Wirklich schade, dass ich diesen Thread erst jetzt sehe.
Ich habe ihn mal überflogen. es wird hier sehr viel gerechnet, es gibt aber auch viel Unsicherheit.
Die ganze Rechnerei anhand der angegebenen Empfindlichkeit und der Enstufenleistung und Anzahl der Lautsprecher Chassis ist nicht ganz verkehrt, aber trotzdem praxisfern.
Als Erstes ist die Angabe der Empfindlichkeit wichtig. Da gibt es für die Hersteller viel Spielraum zum Tricksen.
Üblich sind die Angaben dB/1W/1m oder dB/2,83V/1m. Die Angabe bezieht sich auf den Pegel bei 1kHz. 2,83V an 8 Ohm ergeben ein Watt. Gibt man die Empfindlichkeit in db/2,83V/1m an, kann man ein 4 Ihm Chassis mit 3dB mehr angeben, als ein 8 Ohm Chassis, denn bei der gleichen Spannung nimmt das 4 Ohm Chassis doppelt so viel Leistung auf. Die Angabe ist aber näher an der Praxis, da ein 8 Ohm Chassis keineswegs einfach nur 8 Ohm hat. Es geht hier um eine Impedanz, nicht um einen Widerstand, der Widerstand verändert sich also über die Frequenz. Eine 8 Ohm Angabe bedeutet nur, dass das Impedanzminimum (also der niedrigste Widerstand) nicht niedriger als 6,4 Ohm liegt, es darf also um 20% abgewichen werden. Für ein 4 Ohm Chassis läge das zulässige Minimum folglich bei 3,2 Ohm. Das Minimum liegt normalerweise ober und unterhalb der Resonanzfrequenz.
Zu Verdeutlichung verlinke ich mal das Datenblatt des Eminence Wizard-8. Das soll keine Werbung sein, ich habe dieses Chassis gewählt, weil ich es demnächst verbauen will.
Zum Vergleich noch ein Link zum Datenblatt des Jensen P12Q, der sich in wesentlichen Punkten vom Wizard unterscheidet, aber dazu später mehr.
http://images4.thomann.de/pics/prod/180998_specs.pdf
http://www.etronic-parts.com/data/JP12Q8.pdf
Die Datenblätten enthalten viele Informationen, wenn auch nicht alle.
Man sieht beim Wizard deutlich den verlauf der Impedanzkurve (hellgrau). Die steile Spitze bei 90Hz kommt von der Resonanzfrequenz. jedes Feder-Masse System hat eine Resonanzfrequenz. Bei einem Lautsprecher ist die Membran mit Schwingspule und alles was mit bewegt wird die Masse, Zentrierspinne und Sicke geben die Härte der Aufhängung vor. Wie die Resonanzspitze aussieht hängt von verschiedenen Faktoren ab. Die Stärke des Antriebs, Verluste in der Aufhängung (zum beispiel durch zähe Materialien) und im Antrieb formen die Spitze. Die Kurve im Datenblatt gilt nur für offene Gehäuse, andere Gehäuse verschieben und modellieren die Spitze, oft kommen auch weitere Spitzen dazu, ich will da jetzt nicht näher ins Detail gehen.
Der Anstieg der Impedanz zu hohen Frequenzen kommt von der Induktivität der Schwingspule. Die kleinen Spitzen und Einbrüche in der ansteigenden Kurve deuten auf Resonanzen der Membran hin. Dass sie sich akustisch bemerkbar machen sieht man an den dazu passenden Spitzen und Einbrüchen im Frequenzgang. Bei einem Hifi Lautsprecher ist man bemüht, solche Resonanzen durch Formgebung und Materialwahl bei der Membran zu unterdrücken oder zu höheren Frequenzen außerhalb des angestrebten Wiedergabebereichs zu verschieben. Bei Gitarrenlautsprechern gelten andere Regeln. Die Verfärbungen sind erwünscht, der Lautsprecher für Gitarrenboxen soll im Gegensatz zu einer Hifi Box einen Eigenklang mit bringen.
Nun komme ich zur Frage, warum die reine Empfindlichkeitsangabe zur Einschätzung nicht reicht.
Der Hersteller kann tricksen, ohne zu lügen.
Normalerweise wird der Wert bei 1kHz angegeben, selten gibt ein Hersteller einen anderen Wert an, gerade bei einer Spitze im Frequenzgang, die höher liegt.
Misst man an 1W/1m, kann man hin gehen und die Spannung anheben, bis man 1W bei 1kHz erreicht, wo die Impedanz schon viel höher liegt, also bei 2,83V viel weniger Strom fließen würde. Meistens wird ein 8 ohm Lautsprecher trotz der Angabe 1W/1m an 2,83V gemessen.
Der Hersteller kann anhand der Parameter des Chassis, also der TSP (Thiele Small Parameter) den Wert errechnen. Diese Parameter haben bei so einem Chassis bei 1kHz aber eine untergeordnete Bedeutung, da der Antrieb dort schon nicht mehr viel Zählt und die Membran bei so hohen Frequenzen eh macht, was sie will (Resonanzen), was mit den TSP gar nicht erfasst werden kann. Der so errechnete Wert ist also in der Praxis nicht relevant, die TSP gelten nur für den Bereich um die Resonanzfrequenz herum. So ein errechneter Wert ist also Nonsens.
Im Tieftonbereich spielen nur die TSP und das Gehäuse eine Rolle, das Verhalten im Gehäuse kann man mit einem geeigneten Simulationsprogramm recht genau vorhersagen. Erhebliche Abweichungen vom Verlauf im Datenblatt sind an der Tagesordnung. Wenn das jemanden interessiert, zeige ich das auch mal.
Selbst wenn 2 Lautsprecher nach dem gleichen Verfahren vermessen wurden und bei 1kHz ähnlich laut sind, kann der subjektive eindruck ganz anders ausfallen.
Der Jensen liefert bei tiefen Frequenzen c.a 100db wie der Wizard, bei 2kHz ist er fast genau so laut, trotzdem wirkt er viel leiser, als es der Unterschied bei 1khz vermuten ließe. Der Grund dafür ist der tiefe Einbruch in den Mitten, verursacht durch den schwachen Antrieb des Alnico Jensen.
Nun kann man mit Belastbarkeit und Empfindlichkeit ausrechnen, wie laut ein Lautsprecher spielen kann und tappt zugleich in die nächste Falle.
Die in watt angegebene Belastbarkeit (also die elektrische Belastbarkeit) gibt nur an, bei welcher Leistung die Schwingspule durch glüht. Auch bei dieser Angabe kann man viel tricksen, die Art des Anregungssignals, die Umgebungstemperatur und der Zeitraum sind nur ein paar Stellschräubchen, an denen man als Hersteller drehen kann, um auf hohe Werte zu kommen. Zum Glück ist die elektrische Belastbarkeit in der Praxis meistens nicht relevant. Nur bei sehr geringer Belastbarkeit wird eine zu geringe elektrische Belastbarkeit zum Problem.
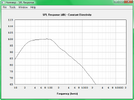
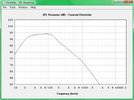
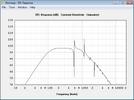
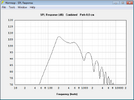
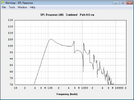
Den Jensen nehme ich daher mal als Beispiel her, da seine elektrische Belastbarkeit nicht besonders hoch ist. Er ist mit 40 Watt Dauerbelastbarkeit und 95db Empfindlichkeit angegeben. Man käme anhand dieser Werte auf einen maximalen Pegel von 111dB. Dieser Lautsprecher wird üblicherweise in einer offenen Box betrieben. Ich wähle für mein Beispiel eine offene, 50x40cm große Box mit 30cm Tiefe.
Daraus ergibt sich bei einer auf dem Boden stehenden Box (Halbraumbedingungen) folgender Verlauf:
Anhang anzeigen 285548
Ich habe Hornresponse zum Simulieren verwendet. dass der Hochton in der Simulation fehlt, liegt daran, dass dieser fast ausschließlich durch membranresonanzen erzeugt wird, die das Programm nicht erfassen kann.
Das Bild zeigt den Verlauf an 2,83V.
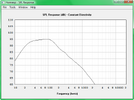
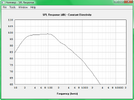
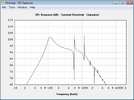
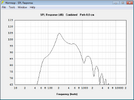
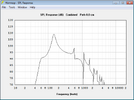
Die gleiche Simulation mache ich nun für den Wizard, der mit 103dB und 75W angegeben ist und laut Empfindlichkeit+Belastbarkeit 119dB schaffen müsste.

Es fällt auf, dass der Wizard in der offenen Box kaum zu tiefen Tönen fähig ist, der Jensen beherrscht das viel besser.
Der Grund ist in den Datenblättern zu finden, der Jensen hat aufgrund des schwachen Antriebs eine viel höhere Gesamtgüte (Qts). Das führt normalerweise zu einem mächtigen Buckel um die Resonanzfrequenz herum, wie man es im Frequenzgang auf den Datenblatt auch schön sehen kann. Da man im offenen Gehäuse unten rum Pegel verliert, ergibt sich beim Jensen ein recht ausgewogener, tief reichender Verlauf. Der Wizard schafft das nicht, er ist aber auch ganz anders ausgelegt, wie anhand der Parameter ersichtlich ist. Ein geschlossenes oder ventiliertes Gehäuse wäre dafür wohl die bessere Wahl, wenn die 80Hz der tiefen E-Saite noch voll zur Geltung kommen sollen.
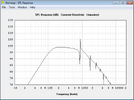
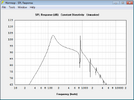
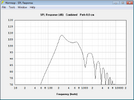
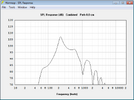
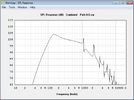
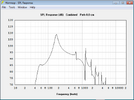
Jetzt wird es interessant, ich simuliere den Maximalpegel der beiden Lautsprecher. Oben der Jensen, unten der Eminence.
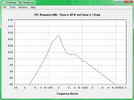
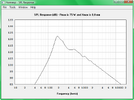
Trotz der fast doppelt so hohen Belastbarkeit und dem großen Unterschied der Empfindlichkeit kann der Wizard unter 150Hz keinen Vorteil heraus arbeiten, der jensen ist sogar geringfügig lauter. Von den errechneten Pegeln bleibt bei tiefen Frequenzen nicht viel übrig. Den Grund findet man wieder in den Datenblättern, nämlich den Wert Xmax, der die maximale lineare Auslenkung der Membran beschreibt. Beide liegen bei etwa einem mm. So weit kann sich die Membran raus und rein bewegen, ohne dass der Antrieb an Kraft verliert und es zu hohen nichtlinearen Verzerrungen kommt, die sich nicht schön anhören. Der Anstieg der Verzerrungen ist nicht sprunghaft, man kann beide auch etwas über Xmax hinaus betreiben, ohne dass es gleich grausam klingt.
Man sieht also, dass Rechnerei in der Praxis nicht sinnvoll ist, wenn man den limitierenden Faktor außer Acht lässt. Bei tiefen Frequenzen ist das die mechanische Belastbarkeit, in diesem Fall der lineare Hub. Subjektiv wird der jensen leiser sein, da er einen tiefen Einbruch in den Mitten hat.
Genug getippt für heute.




 .
. 
