Phasenverschiebung (allg.) ist keine Verpolung, aber eine Phasenverschiebung aller Fourierkomponenten um 180° (Pi) entspricht einer Verpolung. Das lässt sich mathematisch nachweisen.
Nur lässt sich das für sowas wie diese Verzerrung graphisch nicht darstellen.
Nehmen wir mal ein Signal aus zwei Fourierkomponenten (Grundton und Oktave) y=sin(t)+sin(2t) :
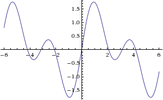
Nun ist deine Vorgehensweise, das komplette Ding um t=Pi zu verschieben sin(t+Pi)+sin(2(t+Pi)):
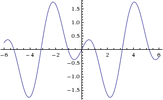
Das ist nicht das invertierte Signal, aber es war auch eine Zeitverschiebung und keine Phasenverschiebung!
Denn wenn man das zerlegt, hast du sin(x+Pi)+sin(2x+2*Pi)) die Harmonische um 2*Pi verschoben. Also verschiebst du den Grundton um 180°, die erste Oktave um 360°, die zweite um 720° etc...
Macht man das für jeden Sinus einzeln, jeweils um Pi
Aus dem Grundton sin(t):
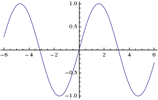
wird sin(t+Pi):
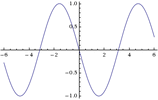
Und aus dem Oberton sin(2t):
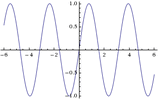
Wird sin(2t+Pi):
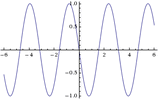
Addiere ich das zusammen sin(t+Pi)+sin(2t+Pi) bekomme ich:
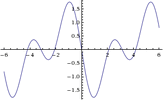
Was genau das invertierte Signal ist.
Das lässt sich nun für beliebige Signale durchführen!
Sorry, aber ich versuche nicht den Lehrmeister heraushängen zu lassen, aber ich mache das jetzt schon 10 Jahre mit zeitabhängigen Signalen in der Elektrotechnik und Nachrichtentechnik, mit Ortskoordinaten in der Physik (Bandmodelle, Potentialtöpfe etc.) zur Beschreibung der elektrischen Eigenschaften von Festkörpern (Halbleitern, Transistoren) etc. Es ist immer das gleiche und ich bin mir da absolut sicher. Jeder Physiker kann das bestätigen.
Das hat auch nichts mit dem Forum zu tun!
PS: Dank an
www.wolframalpha.com für die Plots. Diese 'Suchmaschine' sollte jeder einmal ausprobieren. Einfach was eingeben und der sagt einem alles dazu! z.B. die Formeln oben "(sin(t+Pi)+sin(2t+Pi)) (t from -6 to 6)".
Edit:
Ich hab mich noch mal durch diese Artikel gewälzt. Was dort jeweils nicht verstanden wird:
a) Die haben alle kein periodisches Signal genommen, sondern entweder etwas abschnittsweise definiertes etc. Das kann man auch als Fourierzerlegung beschreiben, aber da kommen noch ganz andere Frequenzanteile rein. (eine Gitarrenseite, die exponentiell in 5 sec. ausklingt, hat dann halt Fourierkomponenten bis 0,2 Hz und weniger (Fourierzerlegung der Exponentialfunktion). Wenn man die auch phasenverschiebt, klappt es wieder.
b) Die haben periodische Signale genommen (Rechteck, Sägezahn etc.) und haben sie
um die Hälfte der Periodizität verschoben, aber nicht für jede Sinusschwingung um die Hälfte
einer Periode der jeweiligen Schwingung.
So kommt diese Fehleinschätzung zusammen.
 )
)







