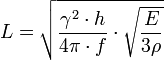Wieviel Auswirkung hat die Hitze auf die Stimmung eines Akkordeons?

[accordion]

Die Schallgeschwindigkeit hat einen Effekt auf die Tonhöhe, wie beim Dopplereffekt hörbar: eine Sirene eines Feuerwehrautos ist höher, wenn es auf einem zufährt (= höhere Schallgeschwindigkeit, der Schall der Sirene trifft schneller auf das Ohr des Hörers), als wenn es von einem wegfährt (= niedrigere Schallgeschwindigkeit). Der Klangerzeuger erzeugt aber immer auf derselben Frequenz.

Realistischerweise ist der Effekt aber nicht sehr gravierend. Die meiste Musik wird wohl im Temperaturbereich 15°-25° gespielt. Wenn das Orchester in sich stimmig ist, ist es mir eigentlich auch egal, ob es mit 440 oder mit 440.5 spielt.

Wenn jemand natürlich das absolute Gehör hat, dann ist dieser Unterschied schon spürbar. Allerdings, so stelle ich mir vor, leiden diese Leute Höllenqualen, wenn ein Orchester mal mit 442 spielt.

Viel schlimmer als die absolute Temperatur ist ein Temperaturanstieg, weil dann die Instrumente unterschiedlich schnell verstimmen. Neulich flüchtete ich deswegen aus einem Konzert.

 

[cknopf]

hallo BE-3

ich vermute, du hast da etwas vermischt, was ich so nicht geschrieben habe:

Zitat von cknopf
bei einer temperaturerhöhung dehnt sich die metallene zunge aus und wird minimal tiefer in der frequenz. wirklich entscheidend für die massive änderung der frequenz nach oben ist jedoch die veränderung der schallgeschwindigkeit durch die temperaturerhöhung.


Zitat von BE-3:
Nee, nee, bei den Stimmzungen wird der Ton doch nicht durch eine schwingende Luftsäule o. ä. erzeugt, sondern von eben der Zunge. Wenn die Frequenz von der Schallgeschwindigkeit abhinge, müßte die Tonhöhe ja etwa um satte 30 (!) Cent ansteigen, wenn die Temperatur von 20 °C auf 30 °C steigt. Das tut sie aber sicherlich nicht!
(Siehe mein obiges Orgel-Beispiel mit dem Vergleich von Zungen- und Labialpfeifen).

ich habe mich auf die von verschiedenen forumsteilnehmern beschriebene frequenzdifferenz von 2-3 cents bezogen. ich habe nirgends geschrieben, dass der ton durch eine schwingende luftsäule erzeugt wird. wieso sollte sich die tonhöhe beim akkordeon bei einer temperaturänderung um 10 grad um 30 cents verändern, es ging doch um drei cents differenz ( wie bereits angeführt) ?

freundliche grüsse

roger

 

[Be-3]

Die Schallgeschwindigkeit hat einen Effekt auf die Tonhöhe, wie beim Dopplereffekt hörbar: eine Sirene eines Feuerwehrautos ist höher, wenn es auf einem zufährt (= höhere Schallgeschwindigkeit, der Schall der Sirene trifft schneller auf das Ohr des Hörers), als wenn es von einem wegfährt (= niedrigere Schallgeschwindigkeit). Der Klangerzeuger erzeugt aber immer auf derselben Frequenz.

Hallo accordion,

das ist völlig richtig. Aber in unserem Fall bewegt sich die Klangquelle (das Akkordeon) nicht in bezug auf den Hörer.
Wenn man sich die Wellenlänge in Luft als Abstand von Druckmaximum zu Druckmaximum vorstellt, dann werden diese Berge "näher zusammengedrängt", wenn man sich auf die Schallquelle zubewegt (oder die Schallquelle sich nähert). Deshalb hören wir dann eine höhere Frequenz (mehr Berge pro Sekunde) und die Tonhöhe steigt.
Umgekehrt (wenn man sich von der Schallquele entfernt) werden die Berge "weiter auseinandergezogen", treffen also mit verminderter Frequenz auf unser Trommelfell und wahrgenommene Tonhöhe fällt.

Solange sich der Akkordeonist nicht auf einem Bürodrehstuhl in schneller Rotation befindet oder auf dem Motorrad vorbeifährt, sehe ich keinen Grund dafür, daß eine Akkordeontonfrequenz von der Schallgeschwindigkeit abhängen sollte.

Du schreibst ja selbst: "Wenn das Orchester in sich stimmig ist, ist es mir eigentlich auch egal, ob es mit 440 oder mit 440.5 spielt."
Eben. Aber es ist ja gerade nicht der Fall, daß sich Instrumente mit unterschiedlicher Tonerzeugung auf gleiche Weise verstimmen, so daß es in sich eben nicht wieder stimmt. Hast Du wirklich noch keine Orgel im Winter gehört, wenn die Kirche die ganze Woche kalt war, am Sonntag geheizt wird und dann die Zungen ("Akkordeon", schwingende Metallzunge) sich kaum verstimmen und die Labialpfeifen ("Flöten", schwingende Luftsäule) aber deutlich?
Wenn alles, wie Du schreibst, hauptsächlich von der Schallgeschwindigkeit abhinge, woher kommt dann dieser Unterschied?

Fazit: Die (tonhöhenbestimmende) Frequenz der Stimmzungenschwingung hängt nicht von der Schallgeschwindigkeit ab.

Exkurs: Unter Wasser
Hat jemand von Euch eines dieser wasserdichten Dusch-Radios? Beim Radio wird die Tonfrequenz durch den schwingenden Lautsprecher erzeugt, sollte also nach "meiner Theorie" nicht von der Schallgeschwindigkeit abhängen.
Unter Wasser breitet sich der Schall über viermal schneller als in Luft aus.
Frage: Erklingt ein Lied aus dem Radio deshalb unter Wasser vier zwei Oktaven höher?
Antwort: Nein. Oder hat jemand andere Erfahrungen gemacht?

hallo BE-3
ich vermute, du hast da etwas vermischt, was ich so nicht geschrieben habe:
[...]
ich habe nirgends geschrieben, dass der ton durch eine schwingende luftsäule erzeugt wird. wieso sollte sich die tonhöhe beim akkordeon bei einer temperaturänderung um 10 grad um 30 cents verändern, es ging doch um drei cents differenz ( wie bereits angeführt) ?

Hallo Roger,

ich wollte Dir keine Aussagen "unterschieben", die Du nicht gesat hast.


Stichwort "Luftsäule"

Die schwingende Luftsäule führte ich nur an, um das klassische Beispiel zu bringen, bei dem eine Tonhöhe von der Schallgeschwindigkeit abhängt, eben weil die durch die Pfeife fest vorgegebene Wellenlänge der stehenden Welle in Verbindung mit veränderter Schallgeschwindigkeit Einfluß auf die Frequenz hat.
Bei der schwingenden Metallzunge haben wir jedoch einen völlig anderen klangerzeugenden Mechanismus. Die Eigenfrequenz der Stimmzunge hängt nicht von der Schallgeschwindigkeit ab, sondern von der Form und den Materialeigenschaften der Stimmzunge.
Ein Federpendel schwingt auch nicht schneller oder langsamer, wenn die Schallgeschwindigkeit sich ändert.

Eine Orgelpfeifenluftsäule schwingt im Vakuum (Weltall) nicht, denn es gibt ja kein Medium (Luft), das dort schwingen könnte.
Eine Akkordeonstimmzunge schwingt im Weltall schon, wenn man sie anzupft (man hört sie bloß nicht ...


Stichwort "Erhöhung um 30 Cent"

Ich gebe Dir recht, Du hast nirgends etwas von 30 Cent geschrieben.
Jedenfalls nicht direkt.
Wenn man aber von Deiner Annahme ausgeht, die Akkordeon-Tonhöhe hinge von der Schallgeschwindigkeit ab, und wenn man sinnvollerweise von einer linearen Abhängigkeit ausgeht, erhält man automatisch den Wert von 30 Cent:

Schallgeschwindikeit in Luft bei 20 °C ist ca. 343 m/s.
Schallgeschwindikeit in Luft bei 30 °C ist ca. 349 m/s.

Wenn man davon ausgeht, daß die erzeugten Töne im selben Verhältnis stehen, erhält man (ob man will oder nicht) einen Faktor von

349/343 = 1,0175...

Das entspricht ungefähr einem Drittelton, nämlich ca. 30 Cent.

Die 30 Cent hast Du zwar nicht erwähnt, aber sie sind eine direkte Folge aus Deiner Schallgeschwindigkeits-Theorie. Oder?

Viele Grüße
Torsten

 

[Piano-Gregor]

Hihihi. Noch besser!!! 3 Cent durch ausgedehnte Luft!!!
Hier der Unterschied

Da hast du Cent und Hertz verwechselt. Aus 440 Hz werden bei 3 Cent mehr 440,75 Hertz.

 

[Klangbutter]

Stimmt, der klassische Fehler...

 

[maxito]

Fazit: Die (tonhöhenbestimmende) Frequenz der Stimmzungenschwingung hängt nicht von der Schallgeschwindigkeit ab.

genau so siehts aus!

Nur deckt sich das halt nicht mit meinen Beobachtungen.
jeder Effekt für sich einzeln ergibt bei Nachrechnung ganz andere Werte, als das was ich beobachte. Drum bin ich mittlerweise der Ansicht, dass das Ganze eine Mischung aus verschiedenen Effketen und Einflüssen darstellt.


Und es ist ja auch so, dass die Stimmplatte nicht völlig ohne Resonanzraum schwingt - Die Stimmplatten sind ja auf Stimmstöcken montiert und die Luft strömt durch die Kanzelle, welche eine bestimmte Länge aufweist und somit auch eine Resonanzfrequenz hat - oder zumindest einen Resonanzbereich. Technisch gesehen haben die wenigsten Kanzellen auch nur ungefähr die richtige Resonanzlänge. Aber mitwirken tut das Ganze schon. Das kann man feststellen, wenn man die Stimmplatte auf eine Prüfkanzelle spannt, bei der man die Kanzellenlänge verändern kann.

Deswegen vermute ich stark, dass die Kanzelle einen Einfluss auf die Frequenz nimmt, wenn auch keinen so großen wie bei Orgelpfeifen.

Hier müsste man mal Messungen mit Stimmplatten machen, die auf einer freien Platte montiert sind, so dass keine Resonaz durch Luftkanallängen mitspielen können und das müsste man dann mal bei verschiedenen Temperaturen wiederholen und schauen, ob ds Ergebnis das gleiche ist, wie bei einem fertig bestückten Akkordeon. Dann kann man zumindest schon mal sehen, ob und wieweit die Kanzelle und Resonanzersacheinungen mitspielen.


Bleibt als Fazit : und sie dreht sich doch! (nach Gallileo Gallilei)

Gruß, maxito

 

[Be-3]

Nur deckt sich das halt nicht mit meinen Beobachtungen.
jeder Effekt für sich einzeln ergibt bei Nachrechnung ganz andere Werte, als das was ich beobachte. Drum bin ich mittlerweise der Ansicht, dass das Ganze eine Mischung aus verschiedenen Effketen und Einflüssen darstellt.

So isses, Maxito,

Die (ohnehin recht wingizen) Effekte heben sich teilweise gegenseitig auf, deshalb ist das Akkordeon ja auch so unverschämt stimmstabil.

Und weil der Einfluß der umgebenden Luft nicht gerade trivial zu berechnen ist, muß wohl tatsächlich das Experiment her...
Mal sehen, was der Haushalt hergibt... es ist ja bald Wochenende.

Viele Grüße
Torsten

 

[cknopf]

hallo zusammen,

ich habe das gefühl, daß sich hier einige sehr sicher sind, dass die schallgeschwindigkeit unerheblich ist für die frequenzveränderung bei wechselnden temperaturen. um nochmals das beispiel des mit helium gefüllten rachenraumes anzuführen: Die tonerzeugung erfolgt im mund- und rachenraum, durch dessen geometrie ist die wellenlänge der schwingung festgelegt. diese geometrie ändert sich bei veränderter temperatur nicht. da ja schallgeschwindigkeit = frequenz mal wellenlänge ist und hier im beispiel die wellenlänge einen festen wert hat, muss sich bei veränderter schallgeschwindigkeit zwangsläufig die frequenz ändern. da die ausbreitungsgeschwindigkeit einer schallwelle in helium ca. 3 mal höher als in luft ist, jedoch die wellenlänge gleich bleibt, ändert sich beim sprechen die tonhöhe, die sprache klingt höher. ich denke (und habe dies auch so schon geschrieben), dass sich dieser effekt auch beim akkordeon und seiner stimmzunge bemerkbar macht und zwar in dem umfang, wie er hier von einigen schon beschrieben wurde, nämlich 2-3 cents bei einer temperaturänderung von etwa 10 grad.

freundliche grüsse

roger

 

[Klangbutter]

 

[accordion]

Der Doppler-Effekt beschreibt streng genommen etwas anderes, ganz klar. Ich dachte, damit lässt sich der Effekt der Schallgeschwindigkeit veranschaulichen.

Alle Recherchen im Internet (wikipedia, sengpielaudio.com, richardschwalbach.de, physikerboard.de) ergeben aber übereinstimmend, dass die Temperatur die Tonhöhe verändert aufgrund der veränderten Schallgeschwindigkeit, unabhängig vom Prinzip der Klangerzeugung (Luftsäule, Saite etc.).

Kennt jemand einen Beleg, dass die Frequenz gleich bleibt, trotz höherer Schallgeschwindigkeit?

 

[Be-3]

ich habe das gefühl, daß sich hier einige sehr sicher sind, dass die schallgeschwindigkeit unerheblich ist für die frequenzveränderung bei wechselnden temperaturen.

Stimmt (für durchschlagende Zungen).
Aber der experimentelle Beweis steht noch aus.

um nochmals das beispiel des mit helium gefüllten rachenraumes anzuführen: Die tonerzeugung erfolgt im mund- und rachenraum, durch dessen geometrie ist die wellenlänge der schwingung festgelegt.
[...]

Das würde also bedeuten: weil der Mund- und Rachenraum die Wellenlänge festlegt, können wir nur in einer Tonhöhe singen bzw. durch die Rachenraumgeometrie festgelegte Naturtöne hervorbringen.

Jetzt aber mal ganz konstruktiv und ernsthaft:

Das Akkordeon ist glücklicherweise in der Lage, auch ohne diesen Resonanzraum Töne zu erzeugen.
Also laß uns doch das Problem dahingehend vereinfachen, daß wir zunächst eimal den Einfluß des Resonanzraums und somit der Schallgeschwindikgeit eliminieren (sind wir uns wenigstens da einig?), indem wir die Temperaturabhängigkeit einer frei auf dem Stimmtisch liegenden Stimmzunge untersuchen.

Bräuchte man nur einen Stimmtisch in einer Klimakammer...

Ich bin der Meinung, das Ansteigen der Tonhöhe hängt mit der Luftdichte und -viskosität zusammen, und zwar in Form eines geringer ausfallenden Dämpfungseffekts (der die Eigenfrequenz des Systems beeinflußt) bzw. des Bernoulli-Effekts, der schließlich die erzwungene Schwingung erzwingt.
Da ich's aber (noch) nicht quantitativ beweisen kann, steht eben momentan Theorie gegen Theorie.

Viele Grüße
Torsten


Ergänzung (wegen accordions Antwort):

Alle Recherchen im Internet (wikipedia, sengpielaudio.com, richardschwalbach.de, physikerboard.de) ergeben aber übereinstimmend, dass die Temperatur die Tonhöhe verändert aufgrund der veränderten Schallgeschwindigkeit, unabhängig vom Prinzip der Klangerzeugung (Luftsäule, Saite etc.).

Diese Stellen habe ich nicht gefunden...
Alle Rechenbeispiele in bezug auf Tonhöhe/Schallgeschwindigkeit beziehen sich immer nur auf stehende Wellen in schwingenden Luftsäulen (Labilapfeifen, Blasinstrumente), aber das trifft ja auf Zungen nicht zu.
Könntest Du Zitate nennen?

"Unabhängig von der Klangerzeugung" ist aber zweifellos falsch. Wo steht das?

Die Temperatur verändert die Tonhöhe der meisten Instrumente mehr oder weniger stark und in verschiedene Richtungen (eben abhängig von der Tonerzeugung).
Aber die Schallgeschwindigkeit ist aber nicht bei allen Instrumenten im Spiel.

Kennt jemand einen Beleg, dass die Frequenz gleich bleibt, trotz höherer Schallgeschwindigkeit?

Was würdest Du als Beweis akzeptieren?


Eine Schallquelle gibt quasi "Druckimpluse" mit einer bestimmten Frequenz ab.

Bei größerer Schallgeschwindigkeit hören wir diese Geräusche früher, aber die Anzahl Schwingungen pro Zeit (und nichts anderes sagt doch die Frequenz aus) bleibt gleich. Wie soll denn eine Änderung der Schallgeschwindigkeit zusätzliche Druckmaxima erzeugen (damit wir einen höheren Ton hören können) oder Druckmaxima verschwinden lassen (damit wir einen tieferen Ton hören)?.

In den Wikipedia-Artikeln "Tonhöhe" oder "Frequenz" kommt das Wort "Schallgeschwindigkeit" nicht einmal vor. Da wird also auf keine grundsätzliche Abhängigkeit zwischen Tonhöhe/Frequenz und Schallgeschwindigkeit hingewiesen. Aber das Wort "Lackfarbe" kommt auch nicht vor.
Welche Stellen meinst Du?

(Ja, ich weiß, die Sache hier dreht sich im Kreis, aber irgendwie müssen wir der Angelegenheit ja auf den Grund gehen)...

 

[cknopf]

hallo BE-3,

schade, dass du es nicht lassen kannst, jeden meiner bisherigen beiträge zum thema in einer überheblichen art und weise zu kommentieren, die den eindruck erweckt, du alleine hast die wahrheit gepachtet. wenn ich das beispiel vom mit helium gefüllten rachenraum anführe, so bedeutet dies in der konsequenz nicht, dass:

zitat BE-3:
Das würde also bedeuten: weil der Mund- und Rachenraum die Wellenlänge festlegt, können wir nur in einer Tonhöhe singen bzw. durch die Rachenraumgeometrie festgelegte Naturtöne hervorbringen.

so etwas hat hier nichts zu suchen; nur wenn jemand partout meine worte missverstehen und falsch interpretieren mag, wird er an deiner art seinen spass haben.

ich befinde mich hier auch nicht in einem wettbewerb, wo es darum geht, wer mehr recht hat; es ist ein forum und es geht darum, anderen zu helfen bzw. dies zu versuchen. ich habe kein problem damit, dass ich mit meiner theorie falsch liege; andererseits habe ich bis jetzt zu diesem thema ausser unbewiesenen theorien und spekulationen noch nichts gelesen, was mich wirklich überzeugt hätte ....

freundliche grüsse

roger

 

[reini2]

ich denke (und habe dies auch so schon geschrieben), dass sich dieser effekt auch beim akkordeon und seiner stimmzunge bemerkbar macht und zwar in dem umfang

dieser Annahme möchte ich widersprechen. Die Bildung des Tones im Kehlkopf-Mundbereich findet anders als in einem Akkordeon statt.
Auf der folgenden Seite http://www.physik.uni-regensburg.de/musik/Poster/helium_lomakina.pdf ist erklärt, daß der Ton zwar durch die Stimmbänder erzeugt wird, aber nachfolgend erst durch die Größe und die Form des Mundraumes gefiltert und Tonhöhenmäßig festgelegt wird. Und nur eine schwingende Luftsäule ändert ihre Frequenz auf Grund geänderter Temoeratur. Die Kanzellen des Akkordeons sind aber so klein, daß sie nicht resonanzfähig sind. Damit bildet sich auch keine schwingende Luftsäule aus.

Gruß
Reini2

 

[Be-3]

Hallo Roger,

tut mir ehrlich leid, wenn meine Kommentare überheblich rübergekommen sind, es war wirklich konstruktiv gemeint...
Im Grunde waren es nichts anderes (so jedenfalls meine Absicht) als Versuche, zu sehen, die gemachten Annahmen konsequent weiterzudenken.

Daß das im Ergebnis natürlich oft stark übertrieben ist, ist mir schon klar - genauso wie meine Schnapsidee, unter Wasser Mundharmonika zu spielen. Es ist aber nicht unüblich, zunächst einmal Extremfälle zu betrachten, wenn man sich Dinge plastisch vor Augen führen möchte.

Ich hatte Dein Rachenraum-Beispiel so interpretiert, wie Du es geschrieben hast: "durch dessen geometrie ist die wellenlänge der schwingung festgelegt".
Was ist dann falsch, wenn ich daraus folgere, daß bei gegebener Schallgeschwindigkeit die Frequenz ebenso festgelegt ist wie die Wellenlänge?


Ziel ist es für mich auch nicht, recht zu haben, sondern eine wirklich plausible Erklärung zu finden.
Notfalls (und darauf läuft es ja hinaus) müssen eben Experimente herhalten, die so aufgebaut sind, daß man den einen oder anderen Effekt bestätigen oder verwerfen kann.
Darum geht's mir, und sonst um nichts.

Laß Dir bitte von mir nicht den Spaß am Board verderben.

Viele Grüße
Torsten

 

[cknopf]

hallo reini2,

ich habe doch schon etliche antworten früher geschrieben:

zitat cknopf:
....ich habe nirgends geschrieben, dass der ton durch eine schwingende luftsäule erzeugt wird.....

freundliche grüsse

roger

 

[accordion]

Vorweg: ich bin kein Physiker und muss nicht unbedingt recht haben. Aber kapiert hab ich es nicht: wenn ich Be-3 richtig verstehe, so gilt für alle Instrumente mit schwingenden Saiten oder Luftsäulen, dass mit höherer Temperatur die Frequenz steigt. Für das Akkordeon gilt das aber nicht, da hier die Schwingung unabhängig vom Medium (Helium, Luft, Wasser, sogar im Vakuum) und Temperatur die Stimmzunge exakt gleich schwingt.

Lässt sich das belegen?

Meinem Verständnis nach braucht die Stimmzunge im Akkordeon einen Impuls, um überhaupt zu schwingen. Das ist üblicherweise die Luft aus dem Balg. Wenn die Temperatur höher ist, ist auch die Schallgeschwindigkeit höher. Die Zunge wird schneller schwingen, was auch einen höheren Ton zur Folge hat. Eigentlich logisch, oder habe ich da was übersehen?

Eventuell ist die Betrachtungsweise auch nicht unbedingt zielführend: eigentlich geht es doch darum, was am Ohr ankommt. Das meinte ich mit "unabhängig von der Erzeugung". Wenn die Schallgeschwindigkeit steigt, so nimmt die Frequenz zu.

 

[ebs]

Es gilt für alle Instrumente mit schwingenden Luftsäulen (nicht Saiten), dass mit höherer Temperatur die Frequenz steigt. Für das Akkordeon gilt das aber nicht, da hier die Schwingung unabhängig vom Medium (Helium, Luft, Wasser, sogar im Vakuum) und Temperatur die Stimmzunge exakt gleich schwingt.
Wenn die Schallgeschwindigkeit der Luftsäule steigt, dann nimmt die Frequenz zu.

Siehe: Tonhöhenänderung durch Temperaturänderung - Einfluss der Temperatur auf die Änderung der Tonhöhe bei Blasinstrumenten (Klarinette, Flöte, Trompete, Orgel) - also nur bei schwingenden Luftsäulen":
http://www.sengpielaudio.com/Rechner-tonhoehenaenderung.htm

Viele Grüße ebs

 

[reini2]

Hallo, Accordion,

ich versuche es mal folgendermaßen zu erklären:
In einer Flöte zum Beispiel wird eine in dem Rohr stehende Luftsäule zum Schwingen gebracht. Die Frequenz dieser Schwingung hängt von der Länge der Luftsäule und von der Ausbreitungsgeschwindigkeit des Schalls in dieser Luftsäule ab. Die Tonerzeugung findet an der Kante statt, gegen die der Luftstrom geblasen wird. Dort entsteht eine Verwirbelung, die den Luftstrom immer hin und her kippen läßt. Die Größe und die Dichte der Luftsäule bestimmen, wie schnell dieses Kippen geschieht. Es entsteht eine sich periodisch ändernde Verdichtung der Luftsäule im Rohr, die Luftsäule gerät in Resonanz. Die Länge des Rohres legt also die Frequenz der Schwingung fest. Wenn die Moleküle der schwingenden Gassäule (beachte die Änderung der Terminologie) beweglicher werden, kann die Frequenz steigen, das scheint logisch. Also erzeugt ein Anblasen mit dem masseärmeren Gas einen höheren Ton, das aber nur bei sonst gleichbleibenden Bedingungen. Da die Masse erwärmter Luft ebenfalls sinkt (Funktionsprinzip Heißluftballon) ergibt sich hier der gleiche Effekt. Um der Frage gleich zu begegnen: der Luftdruck spielt keine Rolle. Luftdruck, Temperatur und Dichte hängen unmittelbar zusammen. Steigender Luftdruck = steigende Tonhöhe, steigende Dichte = fallende Tonhöhe bei gleichbleibender Temperatur. Da bei steigendem Luftdruck die Dichte ebenfalls ansteigt, heben sich die daraus folgenden Tonhöhenänderungen auf.
Soweit die Tonerzeugung durch Anblasen einer Kante.
Die Tonerzeugung durch schwingende: Lippen (Trompete, Horn, Posaune und Co.) legt zunächst den Schluß nahe, dass hier kein Einfluß der Luftsäule besteht, sondern lediglich die Lippenspannung (analog der Saitenspannung einer Gitarre) eine Rolle spielt. Das ist auch zunächst richtig! Das ist aber nur so lange richtig, wie ich nicht die Resonanz einer in einem Rohr eingeschlossenen Luftsäule zur Verstärkung des Tones nutze. Genau das passiert bei den Blechbläsern, sie benutzen ihr Blechrohr zur Verstärkung des mit den Lippen erzeugten Tones. Dabei passen sich die schwingenden Lippen automatisch der Resonanzfrequenz an. Würde man versuchen einen anderen Ton zu blasen, würde der nahezu unhörbar sein, weil keine verstärkende Resonanz der Luftsäule stattfindet. Analoges passiert bei Saxophon, Oboe und Co.. Alle diese Instrumente ändern die Tonhöhe, wenn sich die Temperatur der schwingenden Luftsäule ändert.
Warum tritt dieser Effekt bei Saiteninstrumenten nicht statt? Saiteninstrumente benutzen keine Luftsäule zur Resonanz, sondern eine Holzplatte oder einen Holzkörper, die oder der die Schwingungen der Saite an die umgebende Luft (nicht Luftsäule) weitergibt. Damit ist die Impulsfolge (Frequenz) also ausschließlich von der Saitenspannung und -Länge abhängig. Auch eine höhere Schallgeschwindigkeit in erwärmter Luft ändert das nicht, da die Impulse trotz der erhöhten Transportgeschwindigkeit nur im gleichen Takt beim Ohr ankommen können, wie sie von der schwingenden Saite abgegeben werden.
Und nun nehmen wir die Kurve zum Akkordeon.
Wie in anderen Diskussionen schon besprochen, besitzt das Akkordeon keinerlei Bauteile, die in nennenswerter Weise eine Resonanz ausbilden könnten. Weder einen Resonanzboden, wie ein Klavier, noch eine Luftsäule, wie eine Orgelpfeife. Ein Akkordeon erzeugt seinen Ton allein dadurch, dass die Stimmzunge schwingt und einen Luftstrom ohne Resonanz periodisch unterbricht. Also wird die Schwingung unmittelbar an die umgebende Luft abgegeben eine Filterung der Töne durch Resonanz findet nicht statt. Wenn wir uns diesbezüglich einig sind, haben wir eine ähnlich Situation wie bei den Saiteninstrumenten und damit eine völlige Unabhängigkeit von der Schallgeschwindigkeit respektive Lufttemperatur. Eine Tonhöhenänderung kann also nur mit den mechanischen Bauteilen des Akkordeons zu tun haben. Mit welchen Bauteilen bleibt experimentell zu ermitteln, da kann ich derzeit keine vernünftige und logische Aussage zu machen.
@ accordion

da hier die Schwingung unabhängig vom Medium (Helium, Luft, Wasser, sogar im Vakuum) und Temperatur die Stimmzunge exakt gleich schwingt.

Lässt sich das belegen?

Sieh Dir einmal den Artikel über durchschlagende Zungen in Wikipedia an:http://de.wikipedia.org/wiki/Durchschlagende_Zunge
Da findest Du die folgende Formel, welche den Zusammenhang zwischen Länge und Frequenz einer Stimmzuge beschreibt.

Die Herleitung der Formel macht deutlich, dass ausschließlich die Materialwerte Einfluß auf die Frequenz nehmen.


Vielleicht hilft Dir auch die folgende Überlegung.
Du ersetzt die Impuls gebende Anblasluft durch ein wesentlich massiveres Medium, z.B. einen Finger, der die Zunge zupft. Der Ton wird der gleiche sein. (verzeih bitte dieses etwas grobe Beispiel) .

Ich weiß, dass dies alles schon einmal von dem einen oder anderen geschrieben wurde, aber die Zusammenhänge wurden nicht immer klar. Ich hoffe mit diesem Beitrag etwa Klarheit geschaffen zu haben. Ein paar Skizzen würden die Angelegenheit anschaulicher machen, im Moment bin ich aber durch eine Verletzung der rechten Hand ziemlich am Zeichnen gehindert. Also muß das geschriebene Wort reichen.

Gruß
Reini2


Nachtrag:

eine Stimmzunge, zufällig daliegend, gekühlt auf -10 C erzeugt angezupft den gleichen Ton, wie erwärmt auf ca 50 C, wenn ich dem Korg Gitarrentuner glauben schenken darf. Der "Versuchsaufbau" ist natürlich wenig professionell: Stimmplatte gekühlt/erwärmt auf die Decke einer alten Gitarre gedrückt und angezupft.

 

[Piano-Gregor]

Kennt jemand einen Beleg, dass die Frequenz gleich bleibt, trotz höherer Schallgeschwindigkeit?

Ja: spiele einen Ton auf einem Digitalpiano an und messe diesen mit einem Stimmmgerät. Das machst du 2 mal: bei 10 Grad und bei 30 Grad (und somit bei unterschiedlichen Schallgeschwindigkeiten). Und dann wirst du feststellen, dass es keinen Unterschied gibt.

 

[Be-3]

Hallo zusammen,

reini2 hat ja eine sehr schöne Zusammenfassung geschrieben.
Zum Thema "Generelle Abhängigkeit der gehörten Frequenz von der Schallgeschwindigkeit (unabhängig von der Tonerzeugung) ja/nein" habe ich mal eine kleine Animation zusammengebastelt.

Für das Akkordeon gilt das aber nicht, da hier die Schwingung unabhängig vom Medium (Helium, Luft, Wasser, sogar im Vakuum) und Temperatur die Stimmzunge exakt gleich schwingt.

Lässt sich das belegen?

Hallo Accordion,

auf jeden Fall gilt: Schwingfrequenz eine Akkordeon-Stimmzunge (oder einer Stimmgabel) hängt im Gegensatz zu schwingenden Lufsäulen (Schallgeschwindigkeit!) und Saiten (Materialdehnung) fast nicht von der Temperatur ab.

Deshalb benutzt man ja auch Stimmgabeln oder für Gitarre auch manchmal Stimmpfeifen, weil sie nur aufgrund ihrer Tonerzeugung ziemlich unabhängig von den äußeren Umständen schwingen und eine erstaunlich zuverlässige Referenz für das Stimmen anderer Instrumente bilden.

Warum es dann doch nicht ganz so temperaturunabhängig ist, liegt erstens an der (wenn auch geringen) Temperaturabhängigkeit der von reini2 erwähnten Materialeigenschaften und zweitens daran, daß die effektive Schwingfrequenz des Systems auch durch eine (temperaturabhängige) Dämpfung durch das umgebende Medium (Luft) beeinflußt wird.
Diese effektive Schwingfrequenz liegt umso weiter unterhalb der ungedämpften Frequenz, je tiefer die Temperatur ist.

Eventuell ist die Betrachtungsweise auch nicht unbedingt zielführend: eigentlich geht es doch darum, was am Ohr ankommt. Das meinte ich mit "unabhängig von der Erzeugung". Wenn die Schallgeschwindigkeit steigt, so nimmt die Frequenz zu.

Ich habe mal versucht, mit einem Plotprogramm (gnuplot) genau diesen Fall zu illustrieren:
Man stelle sich links eine Schallquelle vor, die mit der Frequenz f schwingt und rechts einen Zuhörer, bei dem die erzeugte Schallwelle ankommt.
Dann vergleicht man, ob bei unterschiedlichen Schallgeschwindigkeiten unterschiedliche Frequenzen beim Zuhörer ankommen odern nicht.

Hoffentlich habe ich hierbei alle wesentlichen Punkte Deiner Überlegungen berücksichtigt:

• Unabhängig von der Erzeugung: Egal wie erzeugt, die Schallquelle schwingt mit Frequenz f
• Unterschiedliche Schallgeschwindigkeit: Die rote Welle breitet sich mit der vierfachen Schallgeschwindigkeit der grünen Welle aus
• Physikalischer Hintergrund: Frequenz = Schallgeschwindigkeit / Wellenlänge
• Fragestellung: Welche Frequenz kommt beim Hörer tatsächlich an?

Man sieht die rote Schallwelle, die sich viermal so schnell bewegt wie die grüne Schallwelle: Die roten Berge überholen deutlich die grünen Berge.
Allerdings ist die Wellenlänge der roten Welle auch viermal so groß wie die der grünen Welle.

Interpretation: Die höhere Geschwindigkeit der roten Welle wird durch die im gleichen Maße größere Wellenlänge wieder genau ausgeglichen, so daß der Empfänger exakt die Frequenz hört, die die Klangquelle abgestrahlt hat.
Oder: das "Zappeln" nach oben und unten ist links und rechts genau gleich schnell, völlig unabhängig von der Ausbreitungsgeschwindigkeit.

Ergebnis: Unabhängig von der Schallgeschwindigkeit kommt beim Hörer exakt die Frequenz an, die von der Schallquelle ausgestrahlt wird.

Ich hoffe mal, das war einigermaßen anschaulich und überzeugend.


Viele Grüße
Torsten


PS: mein erster Meßversuch ging schon mal schief, weil ich aus der "tollen Konstruktion" keinen Ton herausbekommen habe...