Waljakov
Registrierter Benutzer
- Zuletzt hier
- 03.01.26
- Registriert
- 25.11.13
- Beiträge
- 944
- Kekse
- 11.099
Hi,
ich versuche mir gerade ein paar Basics in digitaler Signalverarbeitung beizubringen und dachte, ich dokumentiere mein kleines Projekt hier ein bisschen, evt interessiert es ja den ein oder anderen. Vielleicht findet sich ja auch jemand, der sich mit dem Thema auskennt und ein paar Tips geben kann.
Ich geht nicht darum, dass ich ein Tool suche, sondern selbst eins schreiben und dabei was lernen will.
Aufgabenstellung
Ich hab zwei Dateien:
- Source: Eine digital generierte Wav-Datei, im Moment ein einfaches Metronom
- Record: Die Source-Datei hab ich auf mein Smartphone gezogen, dort abgespielt und gleichzeitig mit dem Mic wieder aufgenommen.
Gewünschtes Ergebnis: Ich möchte das Source-Signal aus dem Record-Signal herausrechnen, sodass nur die Geräusche übrig bleiben, die das Microphone neben dem Source-Signal noch aufgenommen hat.
Naiver Ansatz
Mein erster recht naiver Ansatz war, einfach die beiden Wellenformen übereinander zu legen und zu subtrahieren. Dazu habe ich die beiden Signale erstmal grob in Audacity übereinander gelegt und dann ein Tool geschrieben, mit dem sich die Wellen Frame-genau ausrichten lassen und die Amplitude des Signale anzupassen.
Aber wer hätte es gedacht: Das funktioniert überhaupt nicht. Die Wellenformen sind zu unterschiedlich.
Aus Interesse habe ich dann das Record-Signal in 2 Teile gesplittet und die erste Hälfte als Source-Signal und die zweite Hälfte als Record-Signal benutzt und so versucht, die zweite Halfte mit der ersten Hälfte auszulöschen. Ich hab den hier makierten Klick des Metronoms genommen und dort beide Teile übereinander gelegt.

Hier der Klick rangezoomt. In blau das Source-Signal und in orange das Record-Signal.
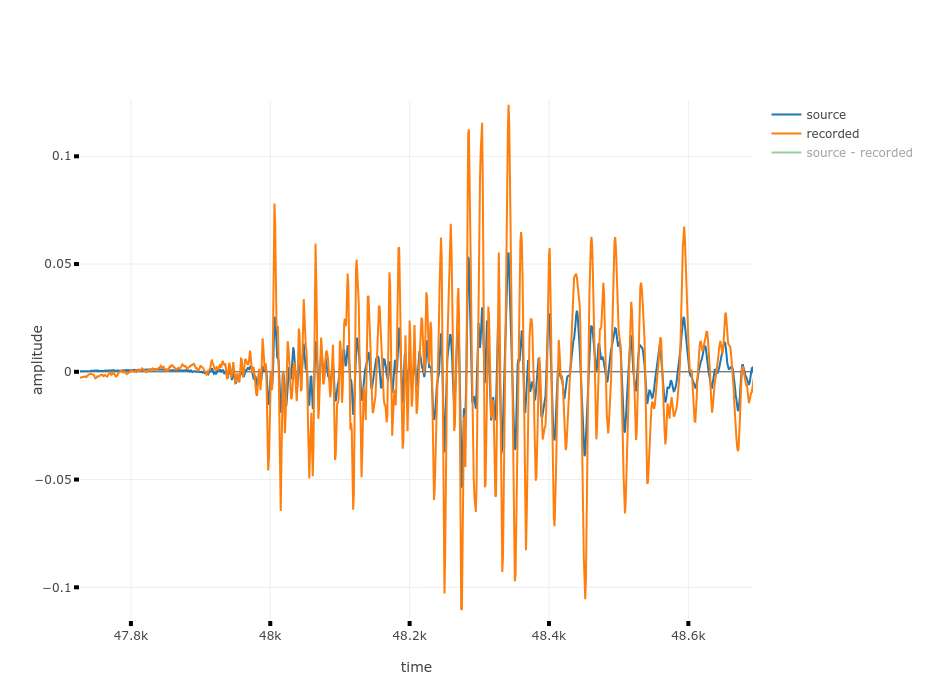
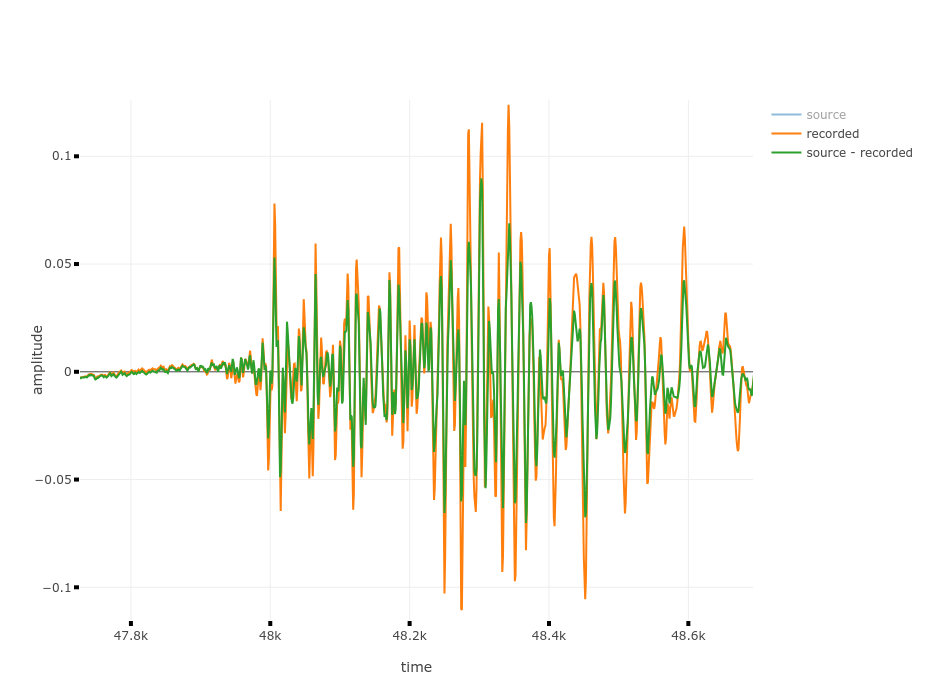
Hier sieht man in Grün das Ergebnis, also die subtrahierten Wellenformen. Im Vergleich zum Record-Signal ist das Ergebnis schon ein Stück leiser geworden. Das kann man auch hören.
Wenn man jedoch zum ersten Klick (siehe Bild1) springt und ranzoomt, sieht man, dass hier die beiden Wellenformen nicht übereinander passen.
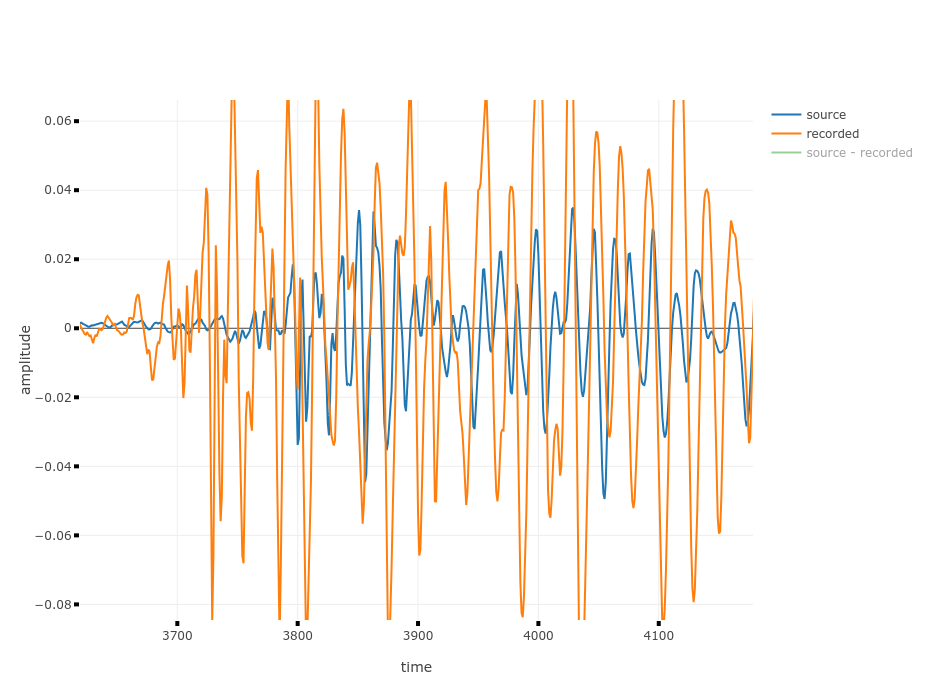
Das sieht man auch am Ergebnis, es tritt kaum Reduktion der Lautstärke auf.
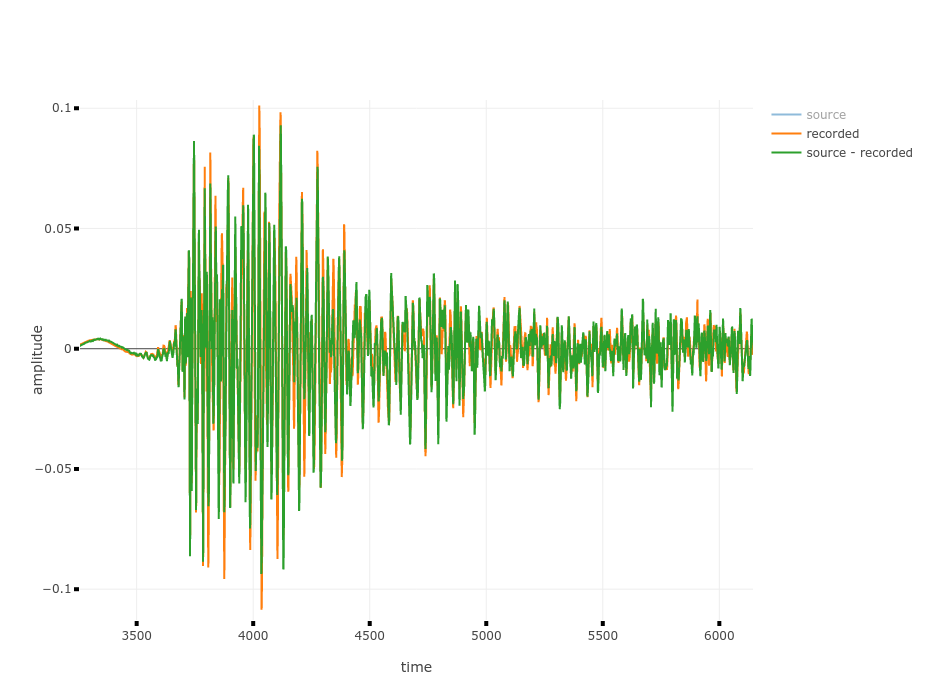
Wenn man sich das Ergebnis anhört, ist also nur der zweite Klick leiser als im Record-Signal, die anderen sind entweder genauso laut oder sogar lauter.
Hätte ich so nicht erwartet.
Fazit: Obwohl es sich um ein digitales, periodisches Signal handelt, führt das Wiederaufnehmen des Signals doch zu einer erheblichen zeitlichen Verschiebung.
Ansatz 2: Spektralanalyse
Im nächsten Schritt will ich jetzt mittels Fourier-Transformation ein Spektrum der Signale erstellen, diese Spektren voneinander subtrahieren und wieder in eine Wellenform umwandeln und schauen, ob das zu brauchbaren Ergebnissen führt.
Das Tool im jetzigen Stand hab ich hier hochgeladen, wer will, kann gerne selbst ein wenig damit herumexperimentieren: https://flappix.github.io/audio_remover/ (braucht nocht ziemlich lang zum Laden, das optimiere ich evt später nochmal)
Mit offset_x und offset_y lässt sich das Source-Signal (blau) ausrichten, mit multiplier kann man es amplifizieren (laut/leiser machen). Im Waveform Plot werden das Source-, Record- und Ergbnis-Signal gleichzeitig angezeigt. Mit einem Klick auf das Signal in der Legende rechts oben lassen sich die einzelnen Signale ausblenden, damit man einen besseren Überblick bekommt. Wenn man mit der Maus über den Plot fährt, sieht man oben eine Menuleiste, mit der man zoomen und verschieben kann.
ich versuche mir gerade ein paar Basics in digitaler Signalverarbeitung beizubringen und dachte, ich dokumentiere mein kleines Projekt hier ein bisschen, evt interessiert es ja den ein oder anderen. Vielleicht findet sich ja auch jemand, der sich mit dem Thema auskennt und ein paar Tips geben kann.
Ich geht nicht darum, dass ich ein Tool suche, sondern selbst eins schreiben und dabei was lernen will.
Aufgabenstellung
Ich hab zwei Dateien:
- Source: Eine digital generierte Wav-Datei, im Moment ein einfaches Metronom
- Record: Die Source-Datei hab ich auf mein Smartphone gezogen, dort abgespielt und gleichzeitig mit dem Mic wieder aufgenommen.
Gewünschtes Ergebnis: Ich möchte das Source-Signal aus dem Record-Signal herausrechnen, sodass nur die Geräusche übrig bleiben, die das Microphone neben dem Source-Signal noch aufgenommen hat.
Naiver Ansatz
Mein erster recht naiver Ansatz war, einfach die beiden Wellenformen übereinander zu legen und zu subtrahieren. Dazu habe ich die beiden Signale erstmal grob in Audacity übereinander gelegt und dann ein Tool geschrieben, mit dem sich die Wellen Frame-genau ausrichten lassen und die Amplitude des Signale anzupassen.
Aber wer hätte es gedacht: Das funktioniert überhaupt nicht. Die Wellenformen sind zu unterschiedlich.
Aus Interesse habe ich dann das Record-Signal in 2 Teile gesplittet und die erste Hälfte als Source-Signal und die zweite Hälfte als Record-Signal benutzt und so versucht, die zweite Halfte mit der ersten Hälfte auszulöschen. Ich hab den hier makierten Klick des Metronoms genommen und dort beide Teile übereinander gelegt.
Hier der Klick rangezoomt. In blau das Source-Signal und in orange das Record-Signal.
Hier sieht man in Grün das Ergebnis, also die subtrahierten Wellenformen. Im Vergleich zum Record-Signal ist das Ergebnis schon ein Stück leiser geworden. Das kann man auch hören.
Wenn man jedoch zum ersten Klick (siehe Bild1) springt und ranzoomt, sieht man, dass hier die beiden Wellenformen nicht übereinander passen.
Das sieht man auch am Ergebnis, es tritt kaum Reduktion der Lautstärke auf.
Wenn man sich das Ergebnis anhört, ist also nur der zweite Klick leiser als im Record-Signal, die anderen sind entweder genauso laut oder sogar lauter.
Hätte ich so nicht erwartet.
Fazit: Obwohl es sich um ein digitales, periodisches Signal handelt, führt das Wiederaufnehmen des Signals doch zu einer erheblichen zeitlichen Verschiebung.
Ansatz 2: Spektralanalyse
Im nächsten Schritt will ich jetzt mittels Fourier-Transformation ein Spektrum der Signale erstellen, diese Spektren voneinander subtrahieren und wieder in eine Wellenform umwandeln und schauen, ob das zu brauchbaren Ergebnissen führt.
Das Tool im jetzigen Stand hab ich hier hochgeladen, wer will, kann gerne selbst ein wenig damit herumexperimentieren: https://flappix.github.io/audio_remover/ (braucht nocht ziemlich lang zum Laden, das optimiere ich evt später nochmal)
Mit offset_x und offset_y lässt sich das Source-Signal (blau) ausrichten, mit multiplier kann man es amplifizieren (laut/leiser machen). Im Waveform Plot werden das Source-, Record- und Ergbnis-Signal gleichzeitig angezeigt. Mit einem Klick auf das Signal in der Legende rechts oben lassen sich die einzelnen Signale ausblenden, damit man einen besseren Überblick bekommt. Wenn man mit der Maus über den Plot fährt, sieht man oben eine Menuleiste, mit der man zoomen und verschieben kann.


