Zweite Heptatonik

[möchtegernbach]

Die lydische Tonleiter entsteht durch Schichtung von 6 reinen Quinten und die anderen Kirchentonleitern sind nur Umkehrungen von dieser.
Wenn man nun lydisch als eine Art "Stammtonleiter" aller 6 anderen Tonleitern ansieht muss es dann nicht auch andere Stammtonleitern geben?
Mir ist aufgefallen dass, zum Beispiel melodisch Moll auch eine lydische Stammtonleiter hat (bloß mit kleiner Septime).
Wie viele mögliche Tonleitern von dieser Art kann es geben und kann man sie irgendwie Hierarchisch ihrer Reinheit nach ordnen? Lydische wäre wohl die mit ihren Modifikationen die reinste weil sie auf reinen Quiten aufbaut. Ich habe bis jetzt 15 Stammtonleitern gefunden (also 105 Tonleitern insgesammt).

 

[Claus]

Wenn man nun lydisch als eine Art "Stammtonleiter" aller 6 anderen Tonleitern ansieht...

Das kommt mir bekannt vor, George Russell schlug in dieselbe Kerbe:
http://www.lydianchromaticconcept.com/lccoto.html

 

[Be-3]

Hallo möchtegernbach,

ob man nun lydisch oder einen der anderen Modi als "Mutter-"/Stammtonleiter ansieht, ist eine Frage der Festlegung.

Ob es aber noch weitere solcher "Stammtonleitern" gibt (und wie viele) ist eine interessante Frage, die sich mathematisch lösen lassen sollte.
Ich schreibe hier "Stammtonleitern" in Anführungszeichen, weil unsere Stammtöne (entsprechend den weißen Tasten beim Klavier) von ihrer Halb-Ganzton-Abfolge festgelegt sind und deshalb alternative Stammtonleitern nicht mehr aus unseren Stammtönen bestünden - das ist aber nur ein begriffliches Problem.


Welche Kriterien muß eine Stammtonleiter erfüllen?

• Vor allem darf sie sich nicht durch eine andere Stammtonleiter darstellen lassen, denn dann wäre sie nur ein Modus dieser anderen Stammtonleiter.
• Beschränken wir uns auf heptatonische (also siebentönige) Tonleitern - das war ja auch die Fragestellung.
• Beschränken wir uns auf Tonleitern, die ausschlielich aus Ganz- und Halbtonschritten bestehen. Das war zwar nicht vorgegeben, aber gehen wir mal davon aus (also kein Hiatus-Sprung oder noch größer).

Für solche Fälle betrachte ich eine Tonleiter immer als Kreis, der in zwölf Halbtonschritte aufgeteilt ist, weil die zyklische Anordnung so schön in sich geschlossen ist, etwa so:




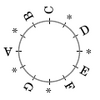Frage: Wie viele Halb- und Ganztonschritte gibt es?

Nennen wir die Anzahl der Halbtonschritte h und die Anzahl der Ganztonschritte g.
Eine siebenstufige Tonleiter muß natürlich aus sieben Stufen bestehen, d. h.

h + g = 7

Außerdem muß "der Kreis geschlossen sein", also die sieben Stufen zusammen müssen 12 Halbtonschritte umfassen:

h + 2g = 12

Nun kann man aufgrund dieser beiden Bedingungen leicht eine eindeutige Lösung für h und g finden:

h = 2
g = 5

Eine Stammtonleiter, die unsere Bedingungen erfüllen will, muß also genau zwei Halbtonschritte enthalten (und folglich genau 5 Ganztonschritte)!

Die verbleibende Aufgabe besteht darin, herauszufinden, auf wieviele Weisen man Halb- und Ganztonschritte anordnen kann, ohne daß Bedingung (I) verletzt wird (durch Drehung der Ringe dürfen verschiedene Stammtonleitern nicht zur Deckung gebracht werden, sonst wäre es ja nur ein Modus einer bereits bekannten Stammtonleiter).

Ich möchte das an dieser Stelle nicht weiter vertiefen, aber man kann leicht ausrechnen (oder ausprobieren), daß es genau drei verschiedene Lösungen gibt, die ich im "Ring-Modell" willkürlich so gedreht habe, daß sie hübsch symmetschrisch aussehen:



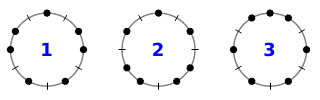
Man erkennt schön, daß keiner der drei Ringe durch Drehung mit einem der anderen zur Deckung gebracht werden kann.
Lösung 1 entspricht übrigens unserer bekannten Stammtonfolge, bei der zwischen den Halbtonschritten immer abwechselnd 2er und 3er-Gruppen mit Ganztonschritten kommen.
Musikalisch sind Lösung 2 und 3 wohl bei uns weniger gebräuchlich...


Ergebnis: Es gibt genau drei solcher Stammtonleitern

Viele Grüße
Torsten

 

[möchtegernbach]

Die zweite Lösung entspricht ja einer Umkehrung von melodisch Moll und die dritte wird wahrscheinlich wegen ihrer aufeinanderfolgenden Halbtonschritte kaum benutzt.
Ich bin ehrlich gesagt mit den selben Kriterien auch auf diese Tonleitern gestoßen nur habe ich im gegensatz zu dir bloß alle Möglichkeiten ausprobiert.
Interessant wäre noch die "Stammtonleitern" ihrem harmonischen Dissonanzgrad zu ordnen. Ich gehe davon aus dass, die Kirchentonleitern den kleinsten Dissonanzgrad von allen möglichen Stammtonleitern (ich benutze den Begriff Stammtonleiter weil er am besten beschreibt was ich meine) haben. Welche von den beiden anderen wäre die zweitreinste? Vielleicht ist doch eine Tonleiter mit Hiatus harmonischer als die beiden welche du gefunden hast?

 

[CUDO II]

Anhang anzeigen 337504

Man erkennt schön, daß keiner der drei Ringe durch Drehung mit einem der anderen zur Deckung gebracht werden kann.
Lösung 1 entspricht übrigens unserer bekannten Stammtonfolge, bei der zwischen den Halbtonschritten immer abwechselnd 2er und 3er-Gruppen mit Ganztonschritten kommen.
Musikalisch sind Lösung 2 und 3 wohl bei uns weniger gebräuchlich...


Ergebnis: Es gibt genau drei solcher Stammtonleitern

2 konsekutive Halbtonschritte gibt natürlich wenig Sinn, wenn man davon ausgeht die Leitern mit terzstrukturierten Akkorden zu harmonisieren.
Lösung 2 ist natürlich ebenso wie Lösung 1 sehr gebräuchlich, unterscheidet sich aber im Tronusgehalt.





Und wenn man den Hiatus als möglichen Stufenschritt hinzuzieht -was man natürlich unbedingt sollte - kommen noch 2 weitere heptatonische Stammtonleitern dazu.

 

[RubenRoeh]

Eine andere m.M. nach sinnvollere Definition ist die von Herrn Haunschild:

Eine Stammtonleiter muss alle Hauptfunktionen erfüllen können.

Hauptfunktionen = Tonika, Subdominante, Dominante

Die Dominante (R-3-5) allein legt für unsere Stammtonleiter schon 3 Töne fest. Die reine Quinte (5) die große Septime (∆7) und die große Sekunde (2). Der Grundton im Abstand einer reinen Quinte ist alleine schon der für das funktionelle Konstrukt essentiellen Quintfallbewegung wegen logisch, die große Terz dieses Akkordes bildet den Leitton und die Quinte vervollständigt den Akkord.

R - 2 (5) - ? - ? - 5 (R) - ? - ∆7 (3)

Die Subdominante (R-3-5/R-b3-5), welche aus funktioneller Sicht sowohl moll als auch Dur sein kann, legt somit zusätzlich die reine Quarte fest.

R (5) - 2 - ? - 4 (R) - 5 - ? (b3/3) - ∆7

Somit bleiben zur "freien" Auswahl nur noch die Terz und die Sexte die jeweils entweder klein oder groß sein können und uns daher die folgenden 4 Möglichkeiten präsentieren:

R - 2 - b3 - 4 - 5 - b6 - ∆7 (harmonisch moll HM)
R - 2 - b3 - 4 - 5 - 6 - ∆7 (melodisch moll MM)
R - 2 - 3 - 4 - 5 - b6 - ∆7 (harmonisch dur HD, enorm selten)
R - 2 - 3 - 4 - 5 - 6 - ∆7 (melodisch dur, oder einfach nur Dur, wie wir das kennen)

Von diesen ausgehend lassen sich genau wie bei der Durtonleiter (Ionisch) jeweils 7 Modi ableiten, welche gerade in der Jazzimprovisation viel Anwendung finden.

Welche Kriterien muß eine Stammtonleiter erfüllen?

• Vor allem darf sie sich nicht durch eine andere Stammtonleiter darstellen lassen, denn dann wäre sie nur ein Modus dieser anderen Stammtonleiter.
• Beschränken wir uns auf heptatonische (also siebentönige) Tonleitern - das war ja auch die Fragestellung.
• Beschränken wir uns auf Tonleitern, die ausschlielich aus Ganz- und Halbtonschritten bestehen. Das war zwar nicht vorgegeben, aber gehen wir mal davon aus (also kein Hiatus-Sprung oder noch größer).

Wieso?