Auch wieder so eine Aussage die ohne jegliches Fundament daherkommt. Das kann man jetzt glauben, oder auch nicht.
Kannst dir auch selbst den Frequenzgang ausrechnen bei gegebenen Filterkoeffizienten

Du hast ja schon zur Website von minidsp verlinkt (übrigens ein Hersteller von DSP Plattformen, ich habe einen Kopfhörerverstärker mit integriertem DSP von ihnen, den ich zum Entzerren meiner Kopfhörer benutze - grandioses Ding), da findest du alles an Material was du brauchst um meine "Aussagen ohne jegliches Fundament" zu überprüfen.
Darfst nur keine Angst vor Mathematik haben, digitale Signalverarbeitung geht nicht ohne komplexe Zahlen.
Aber ich nehme dir die Arbeit mal ab und zeige dir den Frequenzgang eines Peak-Filters ("normaler EQ") mit den Parametern:
Frequenz: 18 kHz
Gütefaktor: Q=2
Gain: 10 dB
Einmal bei einer Samplerate von 44.1 kHz:

Samplerate 48 kHz:
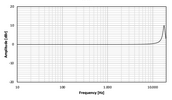
Samplerate 96 kHz:

Samplerate 192 kHz:

Es erweckt den Anschein als ob die Filter eine andere Filtergüte hätten, aber tatsächlich liegt der Güte-Parameter in allen vier Fällen bei Q=2. Die unterschiedliche Filterbreite liegt ausschließlich an der unterschiedlichen Samplerate.
Das betrifft nicht nur Peak-Filter sondern alle biquad-Filterarten.
Als Beispiel hier noch Tiefpass-Filter, die besonders stark davon betroffen sind.
Tiefpass 2. Ordnung bei 10 kHz mit Güte Q=0.71
bei 44.1 kHz Samplerate:
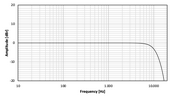
und bei Samplerate 96 kHz:
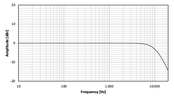
All das macht sich natürlich nicht nur im Frequenzgang des Filters bemerkbar sondern auch in dessen Phasengang, und ist einer der Unterschiede warum man prinzipiell einen Unterschied zwischen 44.1 kHz und 192 kHz Samplerate hören
kann - wenn Biquad-Filter ohne Oversampling verwendet werden.
Advanced Biquad Filter Programming
das list sich überhaupt nicht so als ob die irgendwie minderwertig wären.
Niemand sagt dass sie minderwertig sind, nur dass sie in ihrer reinen Form einen von der Samplerate abhängigen Frequenzgang haben.









