[Frage] Kapsel des Shure Beta 52 a ohmscher Widerstand und Impedanz

[GuywithBass]

Hallo Gemeine,

im Shure Beta 52 a werkelt nicht nur eine spezielle für die Bassdrum optimierte Kapsel, sondern auch noch ein Hardware EQ.

Der Hardware EQ ist ein Kurzschluss aus in Reihe geschalltenen Widerstand (22 Ohm), Kondensator (11 µF aus 2 Stk. 22µF) und eine Spule (15 mH). Daraus ergibt sich eine Bandsperre bei ca. 390 Hz.

Das Mikrofon (Gesamtsystem) hat eine Nennimpendanz (1000 Hz) von 45 Ohm. Leider habe ich keine Möglichkeit Messungen an einem Shure Beta 2a durchzuführen, denn ich habe nur ein Gehäuse ohne Kapsel vorliegen.

Frage: Kann mir bitte jemand den Ohmschen-Widerstand des Shure Beta 52a nennen. Darüber hinaus sind mir auch weitere Messwerte von der Kapsel sehr willkommen.

Gruß

GwB

Kleinen Buchstabensalat im Titel beseitigt. MfG. Basselch

 

[GuywithBass]

In der Hoffnung doch noch ein paar Daten zu bekommen, schiebe ich das Thema mal noch oben.

 

[Etna]

Moin!

Das tut mir leid, aber scheinbar wird es nichts. Kann dir vielleicht jemand besagtes Mikro leihen? Mal in die Runde gefragt?

Es geht ja nur um eine kurze Messung.

Schicken Gruß,
Etna

 

[mikroguenni]

In den technischen Daten ist eine "rated impedance" von 150 Ohm angegeben. Damit liegt der Schwingspulenwiderstand zwischen 80 und 300 Ohm. Bei den meisten in Frage kommenden Shure Kapseln liegt der ohmsche Widerstand bei 280 bis 290 Ohm, ich vermute hier also auch. Dieser Widerstand kann mit einem normalen Ohmmeter gemessen werden.
Der "Hardware EQ" besteht wie schon oben beschrieben aus einer Spule, einem Kondensator und einem Widerstand. Bei der Resonanzfrequenz ist die Impedanz dieses "Saugkreises" theoretisch 22 Ohm, dazu kommen Verluste von Spule und Widerstand, also sind die angegebenen 45 Ohm realistisch.

Ich habe leider kein Beta 52 hier um es durchzumessen.

 

[Etna]

Moin!

Leider werfen die meisten Impedanz und Widerstand in einen Topf, dabei handelt es sich um technisch unterschiedliche Dinge, obwohl beide Angaben mit der Einheit Ohm angegeben werden.

Die Impedanz bezieht sich auf den Wechselstromwiderstand, der meist bei 1kHz gemessen wird. Dies ist auch nur ein Messwert der Gesamtkurve, die als Impedanzverlauf benannt wird. Die Impedanz hängt von der Frequenz ab, sodass es nicht nur einen Wert geben kann. Meist geht dies auch mit einem Phasenverlauf einher, da sich diese verschiebt. Dies leuchtet auch ein, da es sich hierbei um eine Spule handelt.

Ein Widerstand dagegen ist allgemeingültig. Dies egal bei welcher Frequenz oder man eine Gleichspannung (Spezialfall: Frequen beträgt 0Hz.) anlegt.

Jedes passive Bauteil besteht aus einem Widerstand, einer Kapazität und einer Induktivität, da kein Bauteil ideal sein kann. Die jeweils anderen beiden Werte sind parasitär. In diesem Fall, wenn man eine Spule mit einem Ohmmeter durchklingelt, dann misst man nur den (parasitären) Gleichstromwiderstand der Spule und nicht dessen Impedanz im System.

Gerade wenn man Frequenzabhängige Systeme verstehen und planen möchte - und ich vermute @GuywithBass hat dies vor - reicht allein diese Information leider nicht.

Schicken Gruß,
Etna

 

[GuywithBass]

In diesem Fall, wenn man eine Spule mit einem Ohmmeter durchklingelt, dann misst man nur den (parasitären) Gleichstromwiderstand der Spule und nicht dessen Impedanz im System.

Das ist soweit richtig und kann gut berücksichtigt werden. Für ein einfaches Tauchspulenmikrofon (bzw. für die Kapsel) kann als Ersatzschaltbild ein Ohmscherwiderstand in reihe mit einer Induktivität genommen werden. Wenn ich den Durchgangswiderstand (Ohmser) messe und die Impendanze kenne kann ich letztendlich auf die Iduktivität schließen. Mit Fehlern, aber ich habe einen guten Anhalts punkt.

Bei dem Telefunken TD 26 ist z.B. eine Impendanz von 750 Ohm angegeben. Der ohmsche Widerstand liegt bei meinem Exemplar bei 651 Ohm (+/- Fehler).
--- Beiträge wurden zusammengefasst ---

Gerade wenn man Frequenzabhängige Systeme verstehen und planen möchte - und ich vermute @GuywithBass hat dies vor - reicht allein diese Information leider nicht.

Mein Ziel ist es einen Hardware EQ auch für andere Mikrofon (meine Testkandidaten für die Bassdrum) zu bauen um auch einen entsprechenden satten Klang wie den des beta 52a zu bekommen. (Mir ist vollkommen klar, das nicht nur der Hardware EQ den Ton from, sondern auch der mechanisch und insbesondere akustische Aufbau und das Übertragungsverhalten des Beta 52a, bzw. desen Kapsel. Sonst könnte das ja Jeder)

Erster Schritt ist aber die Filterkennlinie des Hardware EQ des beta 52a zu ermitteln. Die Resonszfrequenz des Filters liegt bei ca 392 Hz, ergo eine Bandsperre bei 392 HZ. (C= 11µF, L=15mH). Jetzt versuche ich noch die Eckfrequenzen des Tiefpasses- und des Hochpassanteils und ggf. der Flankensteilheit zu ermitteln um dann das ganzes erst mal mit einem Plug-in in der DAW zu testen. Da das Ganze ein Spannungsteiler ist, geht die Induktivität des Mikrofons gehörig in den Frequenzgang der höhreren Frequenzen ein und formt auch erheblich das Q der Bandsperre. Fröhliche Spielereien mit Excel morgens in der S-Bahn auf dem Weg zur Arbeit sind hier erhellend.

 

[mikroguenni]

Hier findest du eine vergleichbare Frequenzgangentzerrung:

http://www.beyerdynamic.de/shop/media/datenblaetter/DAT_TGD50d_DE.pdf





Oben beyerdynamic, unten Shure


Habe beide Filter mal mit microcap durchsimuliert und einen echten "Screenshot" angehängt.

 

[GuywithBass]

Hier findest du eine vergleichbare Frequenzgangentzerrung:

http://www.beyerdynamic.de/shop/media/datenblaetter/DAT_TGD50d_DE.pdf

Danke! das TGD50 sollte eine ähnliche Kapsel haben wie das Beyerdynamic TG V50d und von daher gleiche messewerte haben.

 

[mikroguenni]

Eines der beiden Bilder hatte sich verflüchtigt, ich habe es dazu gefügt.

Ich denke daß beide Mikrofone die gleiche Kapsel haben.
Ob es die gleiche ist wie im M99 (das war das Urmodell) weiß ich nicht. Da verwirrt mich etwas die Angabe 600 Ohm im Datenblatt.

 

[GuywithBass]

Das mir vorliegende Beyerdynamic TG V50d hat einen Ohmschen Widerstand von Rm= 562 Ohm.

gemäß Thomann:

Richtcharakteristik Niere
50 - 17.000 Hz
600 Ohm

Nach der Betragsformel für den "Komplexen Widerstand"

ZLm(f=1000Hz) = 600 Ohm = Wurzel(Rm²+ XLm²)

und XLm = i*2*Pi*f*Lm

Ergibt sich nach um Formen Lm= Wurzel(ZLm² - Rm²)/(2*Pi*f)

Ergibt sich für die Induktivität des Mikrofon Lm der Wert ca. 33 mH

(Wer einen Denkfehler hier findet und mir das mitteilt bekommt Kekse)

 

[mikroguenni]

Die Kekse hole ich mir heute nachmittag ab, erst mal muß ich mit dem Hund los!

 

[GuywithBass]

@mikroguenni Keksausgabe, aber erst morgen. Ich bin heute vermutlich nicht mehr viel online.

Ps.: Ich lerne gerne dazu!

 

[mikroguenni]

Der Denkfehler ist folgender:

Du gehst davon aus daß das Mikrofon eine Impedanz von 600 Ohm bei 1kHz hat. Gemessen ist davon der ohmsche Anteil 562 Ohm, dann wäre die Differenz zu 600 Ohm durch den induktiven Anteil (von 33mH) verursacht.
Die dazugehörige Rechnung ist zwar richtig durchgeführt, geht aber von falschen Annahmen aus.

600 Ohm als Nennimpedanz beim Mikrofon bedeutet einen (ohmschen) Schwingspulenwiderstand von 600 Ohm. Nur dieser wird angegeben. Der ohmsche Widerstand variiert bei den Mikrofonen, da nicht ein bestimmter Widerstand aufgewickelt wird, sondern bestimmte eine Anzahl Lagen von Kupferlackdraht mit einer bestimmten Spulenlänge. Durch Toleranzen des Kupferlackdrahtes (Durchmesser Kupferdraht mit Toleranz + Dicke des Isolierlackes mit Toleranz + Dicke des Backlacks mit Toleranz) ergeben sich für eine 280 Ohm Spule in der Realität ohmsche Widerstände von 260 bis 300 Ohm je nach tatsächlicher Dicke des Drahtes und der sich daraus ergebenden Anzahl Windungen. Die Abweichung zu den angegebenen 280 Ohm ist NICHT der induktive Anteil.

Bei Andreas Görne "Mikrofone und Theorie und Praxis" ist eine Impedanzkurve abgebildet (beyerdynamic M700 und M59). Seite 171 bei der 1.Ausgabe 1994.
Die Kurve steht zwar auf dem Kopf, man kann aber den Impedanzverlauf gut erkennen. Bei 1kHz ist der Einfluss durch die Resonanzfrequenz noch deutlich höher als der Einfluss des induktiven Anteils.

Morgen, bei mehr Licht werde ich die Kurve mal abknipsen und hier reinstellen. Andreas wird es mir verzeihen.

 

[GuywithBass]

Bei Andreas Görne "Mikrofone und Theorie und Praxis" ist eine Impedanzkurve abgebildet (beyerdynamic M700 und M59). Seite 171 bei der 1.Ausgabe 1994.

Findet sich auch auf Seite 171 bei der 5.Ausgabe 2001 und Seite 164 9. Auflage 2010
--- Beiträge wurden zusammengefasst ---
@mikroguenni

1) Die Kekse bekommst Du!
2) So richtig kann ich Dir aber nicht folgen, da gemäß Vorlesungsskript (hochgeladene PDF) die

Nennimpedanzder "Wechselstromwiderstand bei fester Frequenz (z.B. 1 kHz)" sein sollen.

Warum wird dann von den Mikrofonherstellern der Ohmsche Widerstand angegeben?

Oder willst Du darauf hinaus, das Aufgrund von Fertigungsunterschieden der Ohmsche Widerstand variiert und deshalb auch die Impendanz variiert? Ich also mit der Nennimpendanz keinen festedefinierte werte habe, sondern nur einen Bereich mit eine Varianz von z.B. +/- 10% (540 bis 660 Ohm) habe.
Von dem ein fester Wert von 562 Ohm abgezogen. Es sich von 98 Ohm bis hin zu negativen Werten (welche Unsinn sind) ergeben?

 

[Etna]

Moin!

Bei den Formeln komme ich noch nicht so wirklich klar, weil ich einen Teil der Veriablen noch nicht so wirklich zuzuordnen weis. Vielleicht liegt es an der vorgerückten Stunde...

Sie wirken vielleicht auf einem Stück Papier notiert mit Zusammenhang schlüssiger. Jedenfalls wirkt der berechnete Wert der Spule nicht wirklich fernab der Realität was mit wenigen Wicklungen und der Kapsel als Kern möglich ist.

Bei 1kHz ist der Einfluss durch die Resonanzfrequenz noch deutlich höher als der Einfluss des induktiven Anteils.

Hääääääääääää?! Aber die Resonanz ist doch die Folge der Kombination von Spule und Kondensator im Schwingkreis???

Und im Absatz darüber wird mir nicht wirklich klar ob du nun die Impendanz mit dem ohmschen Widerstand zusammenwirfst oder nicht. Ich versuche das mal aufzudröseln

600 Ohm als Nennimpedanz beim Mikrofon bedeutet einen (ohmschen) Schwingspulenwiderstand von 600 Ohm.

Ja, das ist korrekt, wenn man im Hinterkopf behält, dass diese Angabe bei einer Frequenz von 1kHz gilt.

Nur dieser wird angegeben.

Ja, das ist auch richtig... Nun wird es aber diffus.

Der ohmsche Widerstand variiert bei den Mikrofonen, da nicht ein bestimmter Widerstand aufgewickelt wird, sondern bestimmte eine Anzahl Lagen von Kupferlackdraht mit einer bestimmten Spulenlänge.

Man hat immer und in jedem Bauteil Toleranzen. Aber ich wickel eine Spule? Da wickel ich nicht nach Widerstand, sondern Induktivität.

Das wichtige ist doch der Impedanzverlauf. Also: Welche Frequenz sieht welchen ohmschen Widerstand.
Das soll doch hierbei als Filter heraus kommen.

Durch Toleranzen des Kupferlackdrahtes (Durchmesser Kupferdraht mit Toleranz + Dicke des Isolierlackes mit Toleranz + Dicke des Backlacks mit Toleranz) ergeben sich für eine 280 Ohm Spule in der Realität ohmsche Widerstände von 260 bis 300 Ohm je nach tatsächlicher Dicke des Drahtes und der sich daraus ergebenden Anzahl Windungen. Die Abweichung zu den angegebenen 280 Ohm ist NICHT der induktive Anteil.

Wir wollen aber den Induktiven Anteil heraus finden. Und das können wir ausrechnen, wenn alle anderen Werte gegeben sind und wenn du mit einem Ohmmeter den Gleichstromwiderstand misst, misst du nur den und es hat nichts mit der Impedanz des Mikros zu tun. Diese ist nämlich Frequenzabhängig. Du misst damit nur den einzelnen Wert, der bei der Frequenz von 0Hz vorhanden ist. Der, den der Hersteller angibt, gilt bei 1kHz. Wo ist da jetzt der nötige Zusammenhang?

Oder verstehe ich dich nur absolut falsch und möchtest etwas anderes schreiben?

Schicken Gruß,
Etna

 

[mikroguenni]

Damit wir vom gleichen reden hier erst mal das versprochene Bild der Impedanzkurve:


Es handelt sich um das M700 und das M59 von beyerdynamic. Bei beiden Kurven erkennt man sehr breit und ausgeprägt die (mechanische) Eigenresonanz des Systems zwischen 100 und 200 Hz. Verlgeichbar mit der Lautsprecherimpedanz: http://www.itwissen.info/definition/lexikon/Lautsprecher-Impedanz-loudspeaker-impedance.html
Beim M700: Der Bereich um 1kHz liegt immer noch am Rande des Einflusses der Eigenresonanz. Bei 2kHz ist das minimum der Kurve mit ca. 240 Ohm. Bei 20 kHz liegt die Impedanz bei etwa 260 Ohm.
Beim M59 ist die Impedanz generell höher aber grundsätzlich im Verlauf ähnlich, außerdem erkennt man bei 7kHz einen Einbruch auf Grund eines LRC Filters zur Frequenzgangkorrektur.

(erst mal abspeichern und weiter bearbeiten)
--- Beiträge wurden zusammengefasst ---

Man hat immer und in jedem Bauteil Toleranzen. Aber ich wickel eine Spule? Da wickel ich nicht nach Widerstand, sondern Induktivität.

Die Schwingspule eines Mikrofons hat bestimmte Abmessungen. Der Innen- und Außendurchmesser muß stimmen damit die Spule in den Luftspalt passt. Die Länge der Schwingspule muß auch stimmen damit die Spule sich symmetrisch also mittig im Luftspalt befindet. Die Spule wird also auf einen Dorn aufgewickelt und wird auf eine bestimmte Länge gewickelt. Außerdem werden die Lagen voll gewickelt, also keine halbe Lage. Dann würde der Spulendracht auf einmal in der Mitte der Schwingspule aufhören. Also nicht auf Ohmzahl und auch nicht auf Induktivität.
Ist der Draht mit Lack dünner, ergibt es mehr Spulenwindungen und damit eine höhere Ohmzahl. (und auch höheren induktiven Anteil weil mehr Windungen)

Das wichtige ist doch der Impedanzverlauf. Also: Welche Frequenz sieht welchen ohmschen Widerstand.
Das soll doch hierbei als Filter heraus kommen.

Wir wollen aber den Induktiven Anteil heraus finden. Und das können wir ausrechnen, wenn alle anderen Werte gegeben sind und wenn du mit einem Ohmmeter den Gleichstromwiderstand misst, misst du nur den und es hat nichts mit der Impedanz des Mikros zu tun. Diese ist nämlich Frequenzabhängig. Du misst damit nur den einzelnen Wert, der bei der Frequenz von 0Hz vorhanden ist. Der, den der Hersteller angibt, gilt bei 1kHz. Wo ist da jetzt der nötige Zusammenhang?

Der Impedanzverlauf ist auf dem Meßschrieb aus dem Görne Buch zu erkennen. Der Bereich der höheren Frequenzen wird durch die Induktivität mit beeinflußt.

Das was der Hersteller angibt ist üblicherweise der ohmsche Widerstand. Vielleicht nicht ganz exakt, aber anders kenne ich es nicht.

 

[Etna]

Moin!

Und jetzt wird es noch diffuser, da die mechanischen Eigenschaften eines Schwingungssystems in Resonanz mit der Impedanz eines anderen Schwingungssystem verglichen wird. Das sind alles drei unterschiedliche Dinge!!!

Es kann sowohl elektrisch als auch mechanisch schwingen!!!

Und nein, kein Hersteller gibt einem den ohmschen Gleichstromwiderstand an, sondern die Impedanz bei 1kHz. Das sind unterschiedliche Dinge! Daher weicht das auch voneinander so deutlich ab. Das sind keineswegs die hohen Toleranzen in der Herstellung, sondern schlicht zwei voneinander unabhängige Werte, die zufällig die selbe Einheit in ihren Angaben besitzen.

Der Messschrieb sieht aufgrund der verwendeten Einheiten nicht nach einer Impedanzkurve aus, sondern nach einem Frequenzspektrum, da die Amplitude in dBV angegeben ist.

Also so wie ich das alles lese, wird alles über einen Haufen geworfen was die Nomenklatur der jeweils einzelnen Dinge angeht.

Schicken Gruß,
Etna

 

[GuywithBass]

Das was der Hersteller angibt ist üblicherweise der ohmsche Widerstand. Vielleicht nicht ganz exakt, aber anders kenne ich es nicht.

das würde aber im Grundsatz der Definition der Nennimpendanz wiedersprechen, deren Definition

Nennimpedanzder "Wechselstromwiderstand bei fester Frequenz (z.B. 1 kHz)" sein sollen.

Quelle: Andreas Görne "Mikrofone und Theorie und Praxis".

ist.

Wobei die impendanzkurve nicht nur die rein elektrisch verursachte Impendanz darstellt, sonderm die gesamte Impendanz mit Ihren aktusitischen und mechanischen Anteilen.


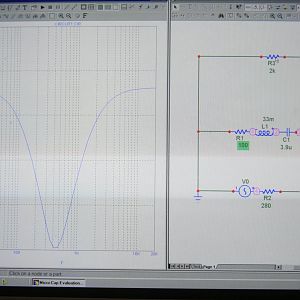
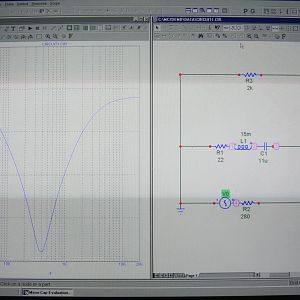
In sofern ist mein Ansatz oben falsch, da die Formel nur den rein elektischen Anteil berücksichtige. Den Akustischen und mechanischen nicht. Das Model, bzw. Ersatzschaltbild (Ohmscher Widrstand, Induktion) gilt daher nicht für meine Nutzung. Tja, dann muss ich halt auf mein LCR (Induktion, Capazitäts und Widerstands) messinstrument warten.

Danke an alle, die mich im Erkenntnisprozess begleitet haben.
--- Beiträge wurden zusammengefasst ---

Und jetzt wird es noch diffuser, da die mechanischen Eigenschaften eines Schwingungssystems in Resonanz mit der Impedanz eines anderen Schwingungssystem verglichen wird. Das sind alles drei unterschiedliche Dinge!!!

Es kann sowohl elektrisch als auch mechanisch schwingen!!!

@Etna , du kamst mir grad zuvor.

 

[mikroguenni]

...
Der Messschrieb sieht aufgrund der verwendeten Einheiten nicht nach einer Impedanzkurve aus, sondern nach einem Frequenzspektrum, da die Amplitude in dBV angegeben ist.
...

Vergiss die vorgedruckten Einheiten links!

Es ist eine Impedanzkurve, als Referenzen sind die 3 Linien 100, 200, 300 und 400 Ohm geschrieben.
(Nur zur Info: die Messung wurde damals von mir durchgeführt)

Nachtrag zur Impedanz: Bei Görne heißt es "Die Nennimpedanz (engl. rating Impedance) ist ein Maß für den frequenzabhängigen elektrischen Widerstand des Mikrofons. Sie wird bei einer Frequenz von 1 kHz bestimmt..."
Hier liegt auch noch eine Ungenauigkeit vor: "rating Impedance" - richtig heißt es rated Impedance ist ein Widerstandsbereich für die Impedanz des Mikrofons. Ein Mikrofon mit 100 Ohm oder 200 Ohm oder 280 Ohm hat eine rated Impedance von 150 Ohm.
Beispiel: Shure SM58:
actual Impedance 300 Ohm, rated impedance 150 Ohm. Quelle Datenblatt http://cdn.shure.com/specification_sheet/upload/82/sm58-specification-sheet-english.pdf
Wobei 300 Ohm die Grenze des Bereichs ist.

 

[mikroguenni]

Ich habe mal eine RL Kombination durchgerechnet: 220 Ohm in Reihe mit 0.5m, 0.8m, 1.1m, 1.4mH um den Anstieg der Impedanz zu hohen Frequenzen festzustellen. Eine Induktivität von 1.1mH ergibt etwa den Anstieg wie in der Impedanzkurve des Mikrofons. (Den Anstieg bei der Resonanzfrequenz habe ich nicht eingebaut, vielleicht ein anderes mal)

Hier ist das Ergebnis: