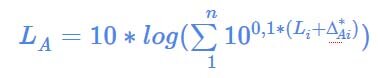L
lusthansa
Registrierter Benutzer
Hallo, Leute. Ich bin Gitarrenlehrer. Ich hatte leider im Abitur damals in Physik leider nicht das Thema "Akustik". Meine Frage dreht sich um Dezibel und die verschiedenen (gibt es das?) Unterformen.
Also: Es ist bekannt, dass Musik auf Dauer die Ohren kaputtmacht, wenn man sie ständig über 85 dB (oder 85 dB(A)??????) hört ...
Daher habe ich mir im Internet ein Lautstärkemessgerät gekauft. Daran ist schon etwas komisch: Es steht unten drauf: Messbereich: 32dB bis ca. 130 dB. Wenn man dann aber das Display anmacht, dann kommt da z. B. 40 dB(A) NICHT 40 dB, wenn man z. B. was leise sagt. Was ist denn nun was bei dB und dB(A)?
Okay, dann zu der Hauptfrage: Ich wohne in einer Wohnung und über mir sind noch Nachbarn. Wir haben das mal, damit´s keinen Streit gibt, getestet, wann die was von mir hören, und das ist bei 85 dB(A) auf der Messgeräteanzeige der Fall. Ist eh super, lauter will ich nicht hören. Okay, nun sagen wir, ich will diese 85 dB(A) erreichen, indem ich das Gitarrenprogramm "Guitar Pro 6" anmache und da eine Spur laufen lasse, die aus allen Noten eines Songs XYZ besteht AUßer (gemutet) der Spur "Rhythmusgitarre". Die habe jetzt mal mein Gitarrenschüler gelernt und will sie über den Guitar Pro - 6 - Backingtrack mir vorspielen. Dabei soll sein Klang (geht ex Line Out vom AMP in mein EPM 6 Mischpult) MIT GP6 zusammen (geht aus dem Audiointerface vom Laptop in meinen Mixer im Stereospurbereich) eben genau diese noch tolerierbaren 85 dB(A) erreichen.
Gut ... jetzt weiß ich noch so nebulös, dass 42,5 dB(A) + 42,5 dB(A) eben NICHT 85 dB(A) sind, sondern dass das was Logarithmisches ist ... Wenn jetzt mein Gitarrenschüler genauso laut sein soll wie der Backing Track, wie muss ich dann beide Regler einstellen? Ist vllt. 82 dB(A) + 82 dB(A) = 85? Oder 83 db(A) + 83 db(A) = 85?? Wer hat da Formeln für?
So, dann noch ne Frage: Guitar Pro 6 hat unten so ein virtuelles Mischpult ... da gibt´s natürlich auch so grafisch dargestellte Fader vom "echten" Mixer ... die kann man hin und herschieben und beim Schieben sieht man dann so Werte wie -0,3 db oder meinetwegen 6.5 db, etc.
Sagen wir mal, beim Song XYZ hat der Rhythmus-Gitarren-Fader in Guitar Pro 6 (und GP6 sei jetzt mal als Noten-Abspieler richtig prima abgemischt ...) die Stellung -3,5 dB(a) ... so: Wie muss ich jetzt mit meinen ganzen Gain und Hastenichgesehenreglern am EPM6 Mixer UND mit den ganzen Reglern am Marshall AMP hindrehen, damit ich GLEICH mit einem perfekten Sound GP6 + echte Gitarre vom Schüler loslegen kann? Ich frage, weil ich will hier keinen Tontechnikunterricht geben,sondern Gitarrenunterricht und der Schüler soll nicht 5 min. bei mir zugucken, wie ich mit seinem Test-Gespiele den "perfekten Mix" hinbiege ... gibt es da so eine "Theorie" zu, die einen gleich per Kopfrechnung die richtigen Settings "rausfinden" lässt oder habe ich da übertriebene Ansprüche?
Danke für Tipps, lusthansa
Also: Es ist bekannt, dass Musik auf Dauer die Ohren kaputtmacht, wenn man sie ständig über 85 dB (oder 85 dB(A)??????) hört ...
Daher habe ich mir im Internet ein Lautstärkemessgerät gekauft. Daran ist schon etwas komisch: Es steht unten drauf: Messbereich: 32dB bis ca. 130 dB. Wenn man dann aber das Display anmacht, dann kommt da z. B. 40 dB(A) NICHT 40 dB, wenn man z. B. was leise sagt. Was ist denn nun was bei dB und dB(A)?
Okay, dann zu der Hauptfrage: Ich wohne in einer Wohnung und über mir sind noch Nachbarn. Wir haben das mal, damit´s keinen Streit gibt, getestet, wann die was von mir hören, und das ist bei 85 dB(A) auf der Messgeräteanzeige der Fall. Ist eh super, lauter will ich nicht hören. Okay, nun sagen wir, ich will diese 85 dB(A) erreichen, indem ich das Gitarrenprogramm "Guitar Pro 6" anmache und da eine Spur laufen lasse, die aus allen Noten eines Songs XYZ besteht AUßer (gemutet) der Spur "Rhythmusgitarre". Die habe jetzt mal mein Gitarrenschüler gelernt und will sie über den Guitar Pro - 6 - Backingtrack mir vorspielen. Dabei soll sein Klang (geht ex Line Out vom AMP in mein EPM 6 Mischpult) MIT GP6 zusammen (geht aus dem Audiointerface vom Laptop in meinen Mixer im Stereospurbereich) eben genau diese noch tolerierbaren 85 dB(A) erreichen.
Gut ... jetzt weiß ich noch so nebulös, dass 42,5 dB(A) + 42,5 dB(A) eben NICHT 85 dB(A) sind, sondern dass das was Logarithmisches ist ... Wenn jetzt mein Gitarrenschüler genauso laut sein soll wie der Backing Track, wie muss ich dann beide Regler einstellen? Ist vllt. 82 dB(A) + 82 dB(A) = 85? Oder 83 db(A) + 83 db(A) = 85?? Wer hat da Formeln für?
So, dann noch ne Frage: Guitar Pro 6 hat unten so ein virtuelles Mischpult ... da gibt´s natürlich auch so grafisch dargestellte Fader vom "echten" Mixer ... die kann man hin und herschieben und beim Schieben sieht man dann so Werte wie -0,3 db oder meinetwegen 6.5 db, etc.
Sagen wir mal, beim Song XYZ hat der Rhythmus-Gitarren-Fader in Guitar Pro 6 (und GP6 sei jetzt mal als Noten-Abspieler richtig prima abgemischt ...) die Stellung -3,5 dB(a) ... so: Wie muss ich jetzt mit meinen ganzen Gain und Hastenichgesehenreglern am EPM6 Mixer UND mit den ganzen Reglern am Marshall AMP hindrehen, damit ich GLEICH mit einem perfekten Sound GP6 + echte Gitarre vom Schüler loslegen kann? Ich frage, weil ich will hier keinen Tontechnikunterricht geben,sondern Gitarrenunterricht und der Schüler soll nicht 5 min. bei mir zugucken, wie ich mit seinem Test-Gespiele den "perfekten Mix" hinbiege ... gibt es da so eine "Theorie" zu, die einen gleich per Kopfrechnung die richtigen Settings "rausfinden" lässt oder habe ich da übertriebene Ansprüche?
Danke für Tipps, lusthansa
- Eigenschaft