sonicwarrior
R.I.P. sonicwarrior
Ausgelagertes OT aus dem Thread Vector-Synthesizer/Vector-Synthese:
Die Beiträge sind aus Gründen der Übersichtlichkeit nicht vollständig zitiert, sondern nur die relevanten Ausschnitte, soweit nicht anders angegeben beziehen sich die Antworten auf die direkt vorher zitierten Beiträge:
#31: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-2#post-7530775
#49: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-3#post-7532533
#66: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-4#post-7534427
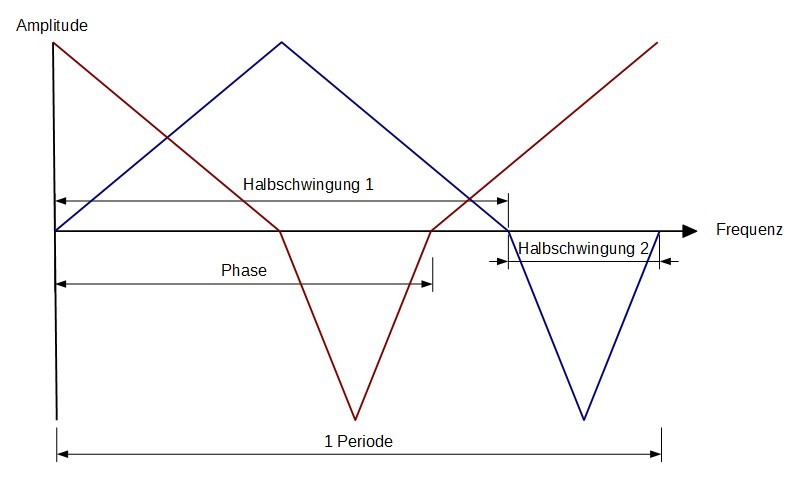
Hier noch die korrigierte Graphik zum Beitrag 62, da es einfacher zu zeichnen war mit Triangle statt Sinus (musste die Schwingung einzeichnen statt aus dem Audio Editor per Screenshot rüber zu kopieren):
Die Beiträge sind aus Gründen der Übersichtlichkeit nicht vollständig zitiert, sondern nur die relevanten Ausschnitte, soweit nicht anders angegeben beziehen sich die Antworten auf die direkt vorher zitierten Beiträge:
#31: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-2#post-7530775
#33: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-2#post-7531034FM ist auch mit niedriger Frequenz noch FM, Vibrato ist FM in einem eingeschränkten Geschwindigkeitsrahmen. Das was bei Yamaha FM heißt ist übrigens eigentlich Phasen Modulation.
#46: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-3#post-7532064Das unterscheidet sich von meinen Informationen. So, wie ich es verstehe, bezieht sich FM (nicht PM) auf zwei Phasen, von denen eine kürzer, die darauffolgende entsprechend länger ist, sodass beide in Summe um einen bestimmten Wert um die Notenfrequenz herumschwingen, je weiter die Frequenzen der einzelnen Phasen von der Notenfrequenz entfernt sind, umso mehr verändert sich der Klangcharakter.
Das hat sich, glaube ich, mittlerweile rumgesprochen. Bei "echtem" FM wird, wie oben beschrieben, die Phasenlänge verändert, während bei PM (Yamaha-FM) der Carrier durch eine oder mehrere weitere Wellen (Operatoren) anderer Form moduliert wird, sich also nicht die Frequenz sondern die Form der Phase verändert.
Höh? Bei Frequenzmodulation wird ganz einfach die Frequenz moduliert. Was Du beschreibst hört sich eher nach PWM = Pulsweitenmodulation an.
Zwei Phasen die um eine Notenfrequenz herum schwingen? Was soll das denn sein?
"Die Form der Phase"? Nee, die Phase selber wird moduliert, siehe:
#49: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-3#post-7532533
#50: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-3#post-7532542Dir scheint nicht bewusst zu sein, wie Wellenlänge und Frequenz zusammenhängen. Gehen wir einmal von a' = 440 Hz bei gleichbleibender Schallgeschwindigkeit aus. Verdoppelt man die Länge der Welle, kann sie in der gleichen Zeit nur noch halb so oft durchlaufen werden, also 220 mal pro Sekunde = 220 Hz, was der Note a entspricht. Da beim Spielen der Note a' jedoch kein a erklingen soll, muss entgegengewirkt werden, indem die folgende Welle entsprechend verkürzt wird, sodass sie die Frequenz 660 Hz erreicht, (220 Hz + 660 Hz) / 2 = 440 Hz = a'. Die eine Welle schwingt also unterhalb von a', die darauf folgende Welle oberhalb von a'. So können in einer Sekunde wieder 440 Wellen durchlaufen werden.
Bei der Pulsweitenmodulation werden nicht die Längen ganzer Wellen verändert sondern die Länge des Wellenberges in Relation mit der des Wellentales, sodass die Länge der Welle selbst gleich bleibt.
Moduliert man eine Phase mit einer anderen Phase, verändert sich die Form der Welle. Als Beispiel nehme ich einen Sägezahn, der mit einem Rechteck moduliert wird:
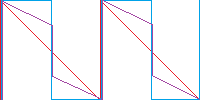
Die Dreickwelle (rot) wird mit einer gleichfrequenten Rechteckwelle (blau) moduliert. Die daraus resultierende Welle entspricht dem Durchschnitt beider Wellen, es entsteht also eine Mischung aus beiden (violett).
#51: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-3#post-7532550...nur ist das, was du gezeichnet hast, im Gegensatz zu der vorangegangenen Erklärung nun gerade weder FM noch VPM, sondern schlicht eine Summierung eines Rechtecks + Sägezahn. Moduliert wird da gar nichts...
Während man sich Frequenzmodulation noch gut vorstellen kann, ist das mit der Phasenmodulation anschaulich nicht so leicht - zumal sie technisch ganz anders funktioniert, aber für das Gehör letztlich sehr ähnliche Ergebnisse liefert. Hier ist das (mit Bildern) ganz gut erklärt: https://www.amazona.de/workshop-ech...ation-lineare-logarithmische-und-phasen-fm/5/
#52: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-3#post-7532956 (Bezieht sich auf Beitrag #49)Nein, die Zeichnung beschreibt eine Phasenmodulation.
Natürlich wird moduliert, nämlich der Sägezahn mit dem Rechteck. Ich empfehle dazu auch den entsprechenden Wikipedia-Artikel, die dortige Grafik der Modulation zweier um 180° zueinander gedrehten Sinuswellen zeigt sehr anschaulich die Veränderung der Wellenform.
#55: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-3#post-7533214 (Bezieht sich auf Beitrag #51)Doch, doch, ich glaube nur langsam, dass wir eine vollkommen inkompatible Ausdrucksweise haben.
Erst sprichst Du von Phasen, jetzt von Wellen. Bitte die korrekten physikalischen Begriffe benutzen, die auch jeder andere verwendet.
Jetzt also Wellenberg/Wellental? Die Dinger heißen Halbwellen bzw. -schwingungen.
=> https://de.wikipedia.org/wiki/Halbschwingung
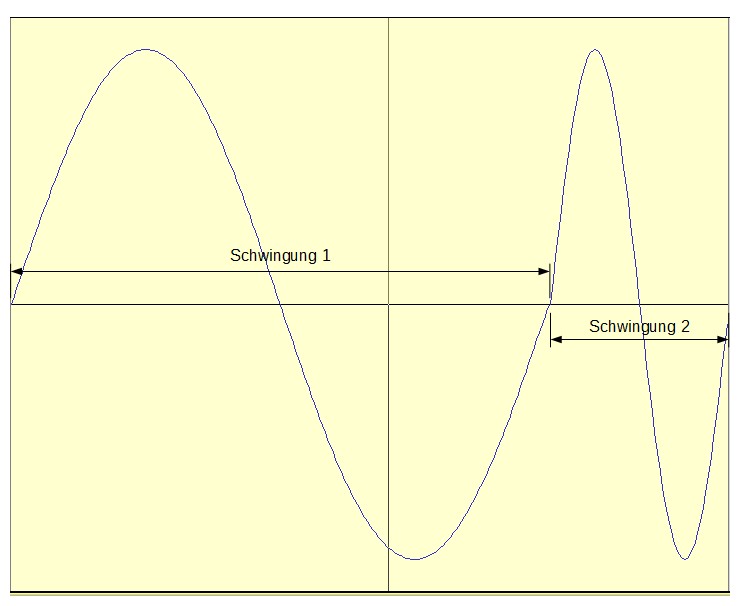
Im vorher zitierten Text scheinst Du auch Halbschwingungen zu meinen, sonst wäre der Text jedenfalls völlig falsch: Zwei vollständige Perioden unterschiedlicher Frequenz ergeben hintereinander keine Note aus der Summe durch Zwei. Siehe Anhang, da habe ich einen 220 Hz Sinus und einen 660 Hz Sinus kombiniert. Einmal vollständige Einzelperioden (d.h. 1 Periode 220 Hz plus 1 Periode 660 Hz) nacheinander und einmal nur die Halbschwingungen (1. vom 220 Hz, 2. vom 660 Hz Sinus). Lad das doch mal einen Sampler mit einem Loop drum rum und hör Dir die beiden mal an oder kopier die Einzel-Zyklen in nem Audio Editor bis ein genügend langes Stück entstanden ist (ist zu groß, um das hier anzuhängen).
2 Phasen sind auch nicht das was Du beschrieben hast.
=> https://de.wikipedia.org/wiki/Phasenverschiebung
Die Länge der beiden Halbwellen hat mit der Phase nichts zu tun, d.h. bei verschobener Phase bleiben die gleich lang.
Es wird nicht eine Phase mit einer anderen moduliert, sondern die Phase einer Schwingung wird von einer anderen Schwingung moduliert.
Die Phase ist quasi der Startpunkt der Schwingung und wird in Grad angegeben (siehe Sinus/Cosinus).
[...] Und bei Frequenzmodulation wird immer noch die Frequenz einer Schwingung durch die Frequenz einer anderen Schwingung moduliert, da passiert nichts mit irgendwelchen 2 "Phasen" oder "Wellen" (was auch immer Du damit meintest), die um eine Note rum schwingen.
#62: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-4#post-7534262 (Graphische Veranschaulichung zu Beitrag #52 bzw. dem dortigen WAV-Anhang)Sorry - nein. Wenn im Sinne der Phasenmodulation der Rechteck den Sägezahn modulieren würde (ich nehme an "oben" beim Rechteck soll 180° und "unten" 0° bedeuten, dann sähe dein Bild so aus:

Resultat wäre ein Sägezahn mit halber Amplitude (+ DC-Offset) und doppelter Frequenz.
Glaub mir, den Artikel kenne ich - und er ist leider für den Anwendungsfall eines Synthesizers, der mittels der technisch einfacheren Phasenmodulation so zu klingen wie ein echter FM-Synthesizer, denkbar ungeeignet zum Verständnis. In dem Artikel geht es letztlich um die Modulation digitaler Daten auf ein Trägersignal - außerhalb der Musik eigentlich der einzig sinnvolle Anwendungszweck.
Und an deinem Verständis des Phasenbegriffs (oder aber der Art das zu beschreiben) solltest du arbeiten, wenn du dich mit dem Thema FM/VPM auseinandersetzen willst: "gedreht" wird da gar nichts. Das ist ein auch bei "Mischpultlern" landläufig vorhandenes Missverständnis, dass eine Polaritätsumkehr irgendwas mit "180° Phase" zu tun hat. Das ergibt ausnahmsweise bei einem reinen Sinus (oder anderen symmetrischen Welleformen) und auch da nur genau beim Spezialfall 180° das gleiche Bild - für andere Signale (bspw. ein Sägezahn) und/oder andere Phasenlagen ist das ein himmelweiter Unterschied.
Weiter oben schreibst du:
Dass bei der Phasenmodulation eine Mischung (zumindest so wie von dir dargestellt) entsteht, ist falsch. Selbst wenn wir annehmen, dass es in deinem Beispiel (zufällig) so wäre, dass Mischung und PM das gleiche Signal ergeben (was nicht so ist, s.o.), dann wäre das eben auch nur in diesem einen und vielleicht einer Handvoll anderer Fälle so - als allgemeine Aussage kann man das nicht so stehen lassen.
Mit einer FM (und letztlich auch mit der PM) erzeugt man vielmehr Seitenbänder, noch am ehesten vergleichbar mit einer Multiplikation der Signale. Das ist der Trick, warum FM beim UKW-Runkfunk so gut funktioniert - man multipliziert das Signal mit der Trägerfrequenz auf a) die doppelte und b) 0 (oder eine Zwischenfrequenz) runter und kann dann mit einem simplen Bandpass 20Hz...20kHz das Audiosignal in hoher Qualität zurückgewinnen (und Amplitudenschwankungen bleiben im Gegensatz zu AM außen vor).
Die 2 Halbschwingungen: 1 mit 220 Hz und 2 mit 660 Hz:
[Anhang gelöscht, weil falsche Darstellung, siehe unten für korrigierte Darstellung, allerdings als Triangle]
Hier die kompletten Perioden hintereinander: Schwingung 1 mit 220 Hz und Schwingung 2 mit 660 Hz.
#66: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-4#post-7534427
#67: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-4#post-7534515Was mich verwirrt ist die Darstellung der "Phasenverschiebung" auf der Zeitachse. Eine Änderung der Phase ohne zeitliche Verzögerung findet quer zur Zeitachse statt und zeigt sich in einer Änderung der Auslenkung zu jenem Zeitpunkt.
#68: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-4#post-7534520Sowohl bei einer zeitlichen Verzögerung als auch bei einer Phasenverschiebung ändert sich das Argument der Funktion, und damit verschieben sich die Nulldurchgänge.
Für eine harmonische Schwingung mit Amplitude A, Frequenz f und Phase phi entspricht eine Verzögerung um d einer Phasenverschiebung um 2*pi*f*d:
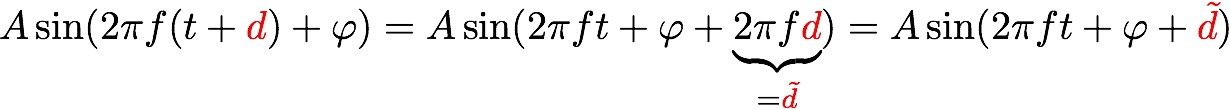
Im Gegensatz zu einer normalen Phasenverschiebung ist die durch die zeitliche Verzögerung entstehende Änderung der Phase frequenzabhängig.
#69: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-4#post-7534522Was ist eine "normale" Phasenverschiebung? Frequenzabhängigkeit besteht in jedem Fall.
#70: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-4#post-7534530In der Praxis vielleicht, da kenne ich mich eh nicht aus. Aber theoretisch kann ich doch ein d-Schlange addieren, das nicht von f abhängt. Das würde ich dann als "normale" Phasenverschiebung bezeichnen.
#71: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-4#post-7534536Du kannst z.B. um 360° drehen oder schieben und es würde sich quasi nichts ändern. Es geht aber gerade darum, dass durch Phasenmodulation eben sich die Frequenzen ändern. Ergo: Abhängigkeit. Eine Phase steht in der Relation zu der Zeit, es gibt immer eine Frequenzabhängigkeit. Wenn man allerdings einen Schnitt in der Zeit macht, dann gibt's eine Phasenänderung ohne Verschiebung. Es ändert sich die Auslenkung.
#72: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-4#post-7534540OK, bei einer Phasenmodulation ist die Verschiebung ja auch nicht konstant, sondern eben selbst ein periodisches Signal.
#73: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-4#post-7534548Eine Änderung der Phase um eine Konstante ändert natürlich nicht die Frequenz, egal wie man die Sache sieht.
"Dein" d-Schlange enthält übrigens in seinem Term die Frequenz f.
#76: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-4#post-7534572Genau diese konstante Verschiebung hat sonicwarrior in seinen Bildern dargestellt.
Wenn man von der zeitlichen Verzögerung her kommt (also die Formel von links nach rechts liest) dann ist das d-Schlange wie gesagt frequenzabhängig. Aber man könnte ja auch einfach eine Konstante addieren, die nicht von der Frequenz abhängt, und so ein phasenverschobenes Signal erhalten. Durch Lesen der Formel von rechts nach links würde man dann eine Delay-Zeit d erhalten, die frequenzabhängig ist: d = d-Schlange/(2*pi*f).
#77: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-4#post-7534584Durch die Änderung der Phase ergibt sich halt ein anderer Kurvenverlauf. Vergleiche z.B. Sinus und Kosinus. Man kann durch die Modulation der Phase die Welle beeinflussen, sie nimmt einen anderen Verlauf an. Man kann durch die Modulation der Phase die Frequenz verändern. Entspricht eine Änderung der Frequenz einer Verschiebung der Kurve? Nein. Die Kurve bekommt einfach einen anderen Verlauf.
#82: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-5#post-7534928Wenn man eine Sinusschwingung phasenmoduliert, so entstehen zusätzliche Teiltöne. Es gibt daher nicht mehr die Frequenz. Das Carrier-Signal kann je nach Wahl des Modulationsindex durchaus weiterhin mit unveränderter Frequenz vertreten sein.
#83: https://www.musiker-board.de/threads/vector-synthesizer-vector-synthese.615593/page-5#post-7534940 (Bezieht sich auf Beitrag #76)Die Phase hat mit der Amplitude erstmal nichts zu tun. Eine Änderung der Phase ohne zeitliche Verzögerung gibt es nicht - oder genauer gesagt, bei einem periodischen Signal (und nur dort ist der Begriff "Phase" überhaupt definiert - und das "startet" nunmal auch nicht irgendwo) macht die Phase erst in Verbindung mit der Zeit einen Sinn. Man kann das völlig äquivalent ineinander umrechnen, wie @synthos schön gezeigt hat. Bei einem Periodischen Signal mit einer bestimmten Frequenz ist die Phase nichts anderes als die Zeitinformation in einer anderen Darstellung. Dass sich bei einer Phasenänderung zu jedem Zeitpunkt auch die Amplitude ändert (wie auch bei einer Zeitverschiebung), ist eine Folge davon.
Mathematisch ist eine Phasenmodulation und eine (bestimmte, aber sehr verbreitete Art der) Frequenzmodulation bis auf einige Details am Rande dasselbe (s. dazu den weiter oben verlinkten Amazona-Artikel).
In der technischen Umsetzung ist es aber ein Unterschied: Im einen Fall benutze ich z.B. einen VCO, dessen Frequenz ich von außen verändere - mit allen Komplikationen, die in dem Artikel sehr schön beschrieben sind. Im anderen Fall benutze ich einen Oszillator, der eine konstante Frequenz abgibt, dessen Phase ich aber von außen einstellen kann. z.B. indem ich einen Generator habe, der sowohl einen sin als auch einen cos erzeugt - mit der richtigen sog. Quadraturmischung kann ich einen Sinus mit beliebiger Phase da herausholen und das sogar mit Steuerspannungen in Echtzeit manipulieren. Wenn das richtig gemacht wird, kann man so aus dem Oszillator im Ergebnis höhere oder niedrigere Frequenzen herausholen als die, mit denen er schwingt. Das lässt sich unterm Strich vor allem besser kontrollieren und wesentlich günstiger herstellen, gerade mit Hilfe von Digitaltechnik - daher der Durchbruch des DX7 damals.
Verstehe nicht was Du damit meinst, ein Kosinus ist Audiotechnisch einfach ein zeitverschobener Sinus. Ich habe den Dr. Octature, der auch ein Sinus-Oszillator mit 8 verschiedenen Phasen ist. Stöpsel ich die 8 Ausgänge jeweils einzeln an den Ausgang klingen die völlig gleich. Die Phase ist nur als Mischung mit anderen Signalen oder untereinander relevant. Sieht man auch im weiter oben im Thread eingebundenen Video zur Phasenmodulation.
Hier noch die korrigierte Graphik zum Beitrag 62, da es einfacher zu zeichnen war mit Triangle statt Sinus (musste die Schwingung einzeichnen statt aus dem Audio Editor per Screenshot rüber zu kopieren):
- Eigenschaft


